HOW TO SOLVE TRIGONOMETRY WORD PROBLEMS
The following steps will be useful to solve word problems in trigonometry.
Step 1 :
Understanding the question and drawing the appropriate diagram are the two most important things to be done in solving word problems in trigonometry.
Step 2 :
If it is possible, we have to split the given information. Because, when we split the given information in to parts, we can understand them easily.
Step 3 :
We have to draw diagram almost for all of the word problems in trigonometry. The diagram we draw for the given information must be correct. Drawing diagram for the given information will give us a clear understanding about the question.
Step 4 :
Once we understand the given information clearly and correct diagram is drawn, solving word problems in trigonometry would not be a challenging work.
Step 5 :
After having drawn the appropriate diagram based on the given information, we have to give name for each position of the diagram using English alphabets (it is clearly shown in the word problem given below). Giving name for the positions would be easier for us to identify the parts of the diagram.
Step 6 :
Now we have to use one of the three trigonometric ratios (sin, cos and tan) to find the unknown side or angle.
Once the diagram is drawn and we have translated the English Statement (information) given in the question as mathematical equation using trigonometric ratios correctly, 90% of the work will be over. The remaining 10% is just getting the answer. That is solving for the unknown.
These are the steps most commonly involved in solving trigonometry word problems.
Things to be Known to Solve Trigonometry Word Problems
To know, how to solve trigonometry word problems, we have to know the following basic things in trigonometry.
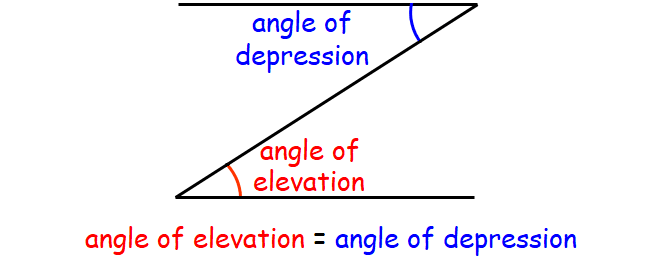
Angle of Elevation and Angle of Depression
Trigonometric Ratios
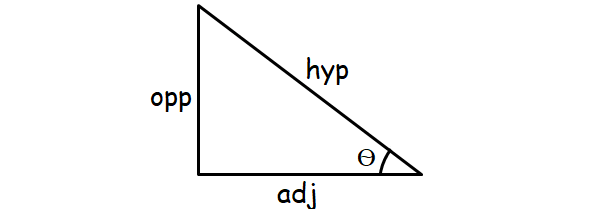
sinθ = opp/hyp
cosθ = adj/hyp
tanθ = opp/adj
opp ----> opposite side
hyp ----> hypotenuse
adj ----> adjacent side
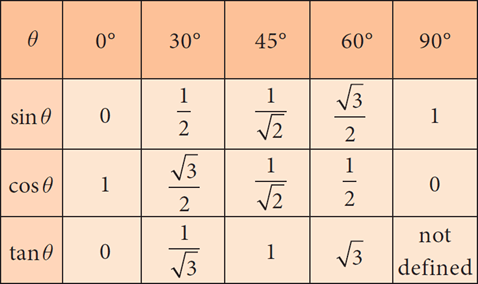
Trigonometric ratios of angles 0°, 30°, 45°, 60° and 90°.
Example :
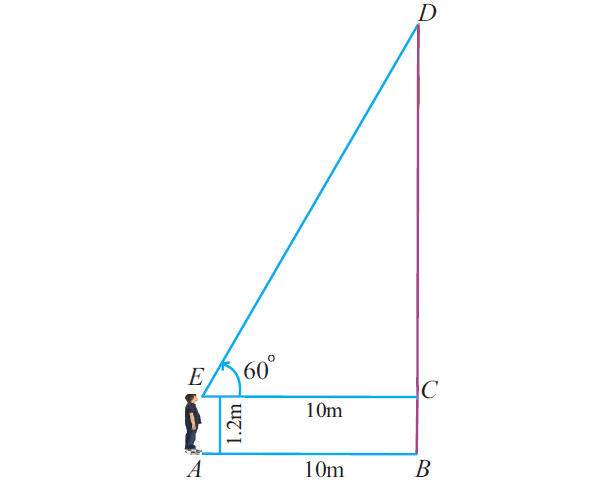
A student stands on the ground at point, which is 10m away from the foot of a pole. He observes the top of the pole at an angle of 60°. Suppose that the height of his eye level from the ground level is 1.2 m , Find the height of the pole.
Solution :
Step 1 :
Let us go through and understand the given information. From our understanding of the information given, we can draw the below picture.
Step 2 :
In the picture drawn above, we have to give name for each position using English alphabets.
That is,
Student position ---> A
Foot of the pole ---> B
Student's eye level ---> E
Top of the pole ---> D
Point on the pole corresponding to eye level ---> C
Now, from the above figure, clearly height of the pole is BD.
And also,
BD = BC + CD
In the picture above, we have
AE = BC
AE = 1.2 m
So, BC = 1.2 m.
Step 3 :
Now, our aim is to get the length of CD.
Once CD is known, easily we can get the length of BD using BD = BC + CD.
Step 4 :
In the right angle triangle CDE, clearly CD is opposite side and EC is adjacent side and it is known to be 10m.
Step 5 :
In the right angle triangle CDE, we have to find the length of opposite side (CD) and the known side is adjacent side (EC = 10m).
Step 6 :
In this problem, we have to use the trigonometric ratio in which we have opposite side and adjacent side. Because, the length of adjacent side (EC = 10m) is known and we have to find the length of opposite side (CD).
Step 7 :
We can use the trigonometric ratio "tan" in this problem. Because, only in "tan", we have opposite side and adjacent side. Now, lets look at, how to find the length of CD.
Step 8 :
tan60° = opp/adj
√3 = CD/EC
√3 = CD/10
10√3 = CD
10 ⋅ 1.732 = CD
17.32 = CD
Step 9 :
The length of the pole BD = BC + CD
BD = 1.2 + 17.32
BD = 18.52
So, the length of the pole is 18.52 m.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
