HOW TO FIND SLANT ASYMPTOTE OF A FUNCTION

Slant Asymptote (Oblique) :

A slant asymptote, just like a horizontal asymptote, guides the graph of a function for for large enough or small enough values of x, that is

x ----> ±∞

But it is a slanted line, that is, neither vertical nor horizontal.

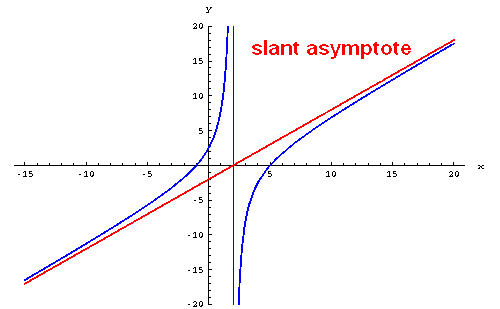
We can find slant or asymptote oblique of a function, only if it is a rational function.

That is, the function has to be in the form of

Rational Function - Example :

Finding the Equation of a Slant or Oblique Asymptote of a Rational Function

Slant asymptote for a rational function will exist, only if the following consition is met.

"If the degree (largest exponent of the variable) of the numerator exceeds the degree of the denominator exactly by one"

To find slant asymptote, we have to use long division to divide the numerator by denominator.

When we divide so, let the quotient be (ax + b).

Then, the equation of the slant asymptote is

y = ax + b

Consider the following situations in a rational function.

Situation 1 :

The degree of the numerator and denominator are equal.

Situation 2 :

The degree of the numerator is less than the degree of the denominator.

Situation. 3 :

The degree of the numerator is greater than the degree of the denominator by more than one. That is, the degree of the numerator is greater than the degree of the denominator by 2 or 3 or 4, etc.

"In all the above situations, there is NO slant asymptote for the given rational function"

In each case, find the slant or oblique asymptote:

Example 1 :

Solution :

In the given rational function, there is no variable in numerator. So, the degree of the numerator is 0. And the degree of the denominator is 1.

Since the degree of the numerator is less than the degree of the denominator, there is NO slant asymptote.

Example 2 :

Solution :

In the given rational function, the degree of the numerator is 2 and the degree of the denominator is 2.

Since the degree of the numerator and the denominator are equal, there is NO slant asymptote.

Example 3 :

Solution :

In the given rational function, the degree of the numerator is 4 and the degree of the denominator is 2.

Since the degrees of the numerator exceeds the degree of the denominator by 2, there is NO slant asymptote.

Example 4 :

Solution :

In the given rational function, the degree of the numerator is 2 and the degree of the denominator is 1.

Clearly, the degree of the numerator exceeds the degree of the denominator exactly by one. So, there is a slant asymptote.

To get the equation of the slant asymptote, we have to divide the numerator by the denominator using long division as shown below.

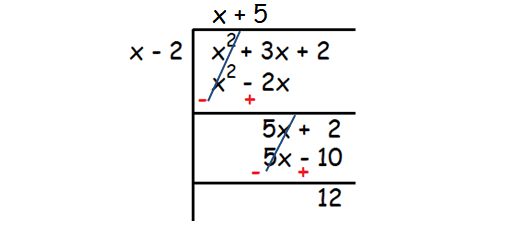
In the above long division, the quotient is (x + 5).

So, the equation of the slant asymptote is

y = x + 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

HOW TO FIND SLANT ASYMPTOTE OF A FUNCTION

Finding the Equation of a Slant or Oblique Asymptote of a Rational Function

Recent Articles

Digital SAT Math Problems and Solutions (Part - 72)

SAT Math Resources (Videos, Concepts, Worksheets and More)

Digital SAT Math Problems and Solutions (Part - 76)