HORIZONTAL TRANSLATIONS OF FUNCTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Horizontal translations of functions are the transformations that shifts the original graph of the function either to the right side or left side by some units.
Definition
A horizontal translation "slides" an object a fixed distance either on the right side or left side. The original object and its translation have the same shape and size, and they face in the same direction.
In simple words, horizontal translation means, it just moves the given figure either on the right or left without rotating, re-sizing or anything else.
Rule

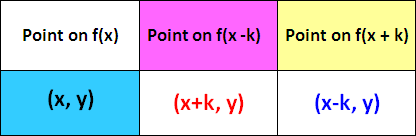
Let y = f(x) be a function and 'k' be a constant.
In the above function, if 'x' is replaced by 'x - k', we get the new function
y = f(x - k)
The graph of y = f(x - k) can be obtained by the translating the graph of y = f(x) to the right by 'k' units if 'k' is a positive number.
In case 'k' is a negative number, the graph of y = f(x) will be translated to the left by |k| units.
Moreover, if the the point (x, y) is on the graph of
y = f(x)
then the point (x + k, y) is on the graph
y = f(x - k)
For example, if k = 3, the graph of y = f(x) will be translated to the right by "3" units.
If k = -3, the graph of y = f(x) will be translated to the left by 3 units.
Example :
Perform the following transformation to the function
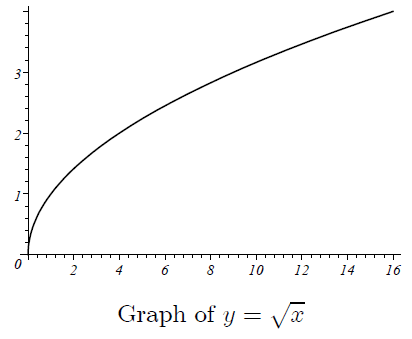
y = √x
"a translation to the right by 3 units"
And also write the formula that gives the requested transformation and draw the graph of both the given function and the transformed function
Answer :
Step 1 :
Since we do a translation to the right by 3 units, we have to replace 'x' by 'x - 3' in the given function
y = √x
Step 2 :
So, the formula that gives the requested transformation is
y = √(x - 3)
Step 3 :
The graph y = √(x - 3) can be obtained by translating the graph of y = √x to the right by "3" units.
Step 4 :
The graph of the original function (given function)
Step 5 :
The graph of the transformed function.
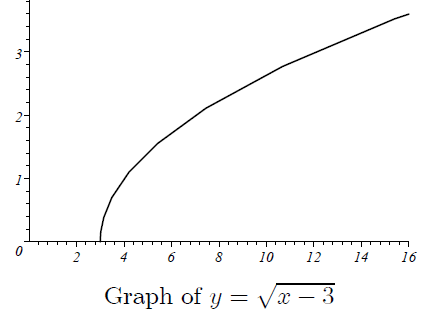
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos -
Times Table Shortcuts
Dec 30, 25 07:14 PM
Times Table Shortcuts - Concept - Examples -
10 Hard SAT Math Questions (Part - 42)
Dec 30, 25 05:52 AM
10 Hard SAT Math Questions (Part - 42)
