HCF AND LCM WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
1. Find the HCF of :
(23 ⋅ 32 ⋅ 5 ⋅ 74), (22 ⋅ 35 ⋅ 52 ⋅ 76) and (23 ⋅ 53 ⋅ 72)
2. Find the LCM of :
(23 ⋅ 33 ⋅ 5), (23 ⋅ 32 ⋅ 52) and (2 ⋅ 3 ⋅ 52)
3. Find the LCM of :
0.63, 1.05 and 2.1
4. Two number are in the ratio 15 : 11 and their HCF is 13. Find the numbers.
5. The HCF of two numbers is 11 and their LCM is 693. If one of the numbers is 77, find the other number.
6. Find the greatest possible length which can be used to measure exactly the lengths 4 m 95 cm, 9 m and 16 m 65 cm.
7. Find the greatest number which on dividing 1657 and 2037 leaves remainders 6 and 5 respectively.
8. Find the largest number which divides 62, 132 and 237 leaves the same remainder in each case.
9. Find the greatest number of four digits which is divisible by 15, 25, 40 and 75.
10. Two numbers are in the ratio 6 : 7. If their LCM is 84, then find the two numbers.

Answers
1. Answer :
In the given numbers, we find 2, 5 and 7 in common.
Take 2, 5 and 7 with minimum power.
That is 22, 5 and 72.
The HCF of the given numbers is
= 22 ⋅ 5 ⋅ 72
= 4 ⋅ 5 ⋅ 49
= 980
2. Answer :
In the given numbers, each base is a prime number.
Take all the different prime numbers with maximum powers.
They are 23, 33 and 52.
The LCM of the given numbers is
= 23 ⋅ 33 ⋅ 52
= 8 ⋅ 27 ⋅ 25
= 5400
3. Answer :
We we look at the given numbers 0.63, 1.05, and 2.1, maximum number of digits after the decimal is 2.
So, let us multiply each number by 100 to get rid of the decimal.
When the given numbers are multiplied by 100, we get 63, 105 and 210.
Now, decompose 63, 105 and 210 into prime factors.
63 = 32 ⋅ 7
105 = 5 ⋅ 3 ⋅ 7
210 = 2 ⋅ 5 ⋅ 3 ⋅ 7
Take all the different prime factors with maximum powers.
They are 2, 32, 5 and 7.
The LCM of (63, 105 and 210 ) is
= 2 ⋅ 32 ⋅ 5 ⋅ 7
= 2 ⋅ 9 ⋅ 5 ⋅ 7
= 630
To get LCM of (0.63, 1.05, 2.1), divide 630 by 100.
630/100 = 6.3
So, the L.C.M of (0.63, 1.05, 2.1) is 6.3.
4. Answer :
From the given ratio, the two numbers can be assumed as 15x and 11x.
HCF of 15x and 11x is x.
Given : HCF of two numbers is 13.
x = 13
15x = 15 ⋅ 13 = 195
11x = 11 ⋅ 13 = 143
So, the two numbers are 195 and 143.
5. Answer :
Let x be the other number.
Product of two numbers = HCF ⋅ LCM
Substitute.
77 ⋅ x = 11 ⋅ 693
x = 99
So, the other number is 99.
6. Answer :
Required greatest possible length is
= HCF (495, 900, 1665)
To find HCF, decompose 495, 900 and 1665 into prime factors.
495 = 32 ⋅ 5 ⋅ 11
900 = 22 ⋅ 32 ⋅ 52
1665 = 32 ⋅ 5 ⋅ 37
In the prime factors of (495, 900, 1665), we find 3 and 5 in common.
Take 3 and 5 with minimum power.
They are 32 and 5.
Then the HCF is
= 32 ⋅ 5
= 9 ⋅ 5
= 45
So, the required greatest possible length is 45 cm.
7. Answer :
Required greatest number is
= HCF of (1657 - 6) and (2037 - 5)
= HCF (1651, 2032)
= 127
So, the required number is 127.
8. Answer :
Required greatest number is
= HCF of (132 - 62), (237 - 132) and (237 - 62)
= HCF (70, 105 and 175)
= 35
So, the required number is 35.
9. Answer :
Greatest number of 4-digits is 9999.
LCM of 15, 25, 40 and 75 is 600.
If a four digit number is divisible by 15, 25, 40 and 75, then the same four digit number should also be divisible by their LCM 600.
On dividing 9999 by 600, the remainder is 399.
To find the greatest four digit number exactly divisible by 600, we need to subtract the remainder 399 from 9999.
9999 - 399 = 9600
Therefore, 9600 is exactly divisible by 600.
Because, 9600 is exactly divisible by 600, the it should also be divisible by 15, 25, 40 and 75.
So, the greatest number of four digits which is divisible by 15, 25, 40 and 75 is 9600.
10. Answer :
From the given ratio, the numbers can be assumed as 6x and 7x.
We can find LCM of 6x and 7x using synthetic division as given below.
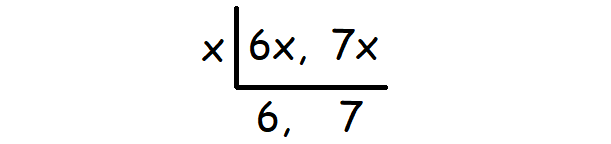
Therefore, LCM of (6x, 7x) is
= x ⋅ 6 ⋅ 7
= 42x
Given : LCM of the two numbers is 84.
42x = 84
x = 2
Substitute x = 2 in 6x and 7x to find the two numbers.
6x = 6 ⋅ 2 = 12
7x = 7 ⋅ 2 = 14
So, the two numbers are 12 and 14.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
AP Precalculus Problems and Solutions
Feb 09, 26 08:43 AM
AP Precalculus Problems and Solutions -
Dilation Transformation
Feb 07, 26 08:30 PM
Dilation Transformation - Concept - Rule - Examples with step by step explanation -
SAT Math Practice Problems Hard
Feb 07, 26 07:37 PM
SAT Math Practice Problems Hard