GRAPHING ABSOLUTE VALUE FUNCTIONS
The following steps will be useful to graph absolute value functions.
Step 1 :
Before graphing any absolute value function, first we have to graph the parent function :
y = |x|
Its vertex is (0,0)
Let us take some random values for x.
x = -3 ----> y = |-3| = 3 ----> (-3, 3)
x = -2 ----> y = |-2| = 2 ----> (-2, 2)
x = -1 ----> y = |-1| = 1 ----> (-1, 1)
x = 0 ----> y = |0| = 0 ----> (0, 0)
x = 1 ----> y = |1| = 1 ----> (1, 1)
x = 2 ----> y = |2| = 2 ----> (2, 2)
x = 3 ----> y = |3| = 3 ----> (3, 3)
If we plot these points on the graph sheet, we will get a graph as given below.
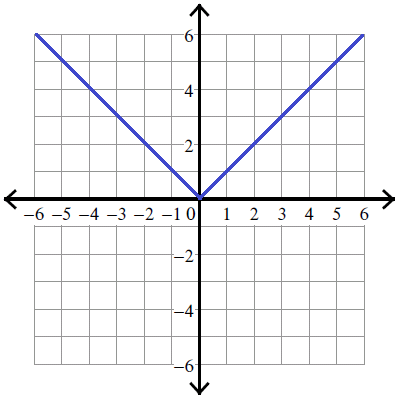
When we look at the above graph, clearly the vertex is
(0, 0)
Step 2 :
Write the given absolute value function as
y = |x - h| + k
Vertex is (h, k).
According to the vertex, we have to shift the above graph.
Note :
If we have negative sign in front of absolute sign, we have to flip the curve over.
Example :
y = -|x|
In each of the following examples, graph the given absolute value function.
Example 1 :
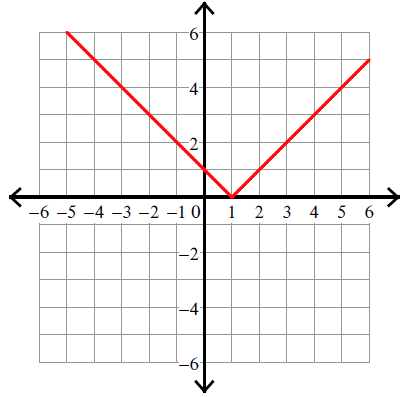
y = |x - 1|
Solution :
y = |x - 1| ----> y = |x - 1| + 0
Compare :
y = |x - h| + k
y = |x - 1| + 0
Vertex (h, k) = (1, 0).
Example 2 :
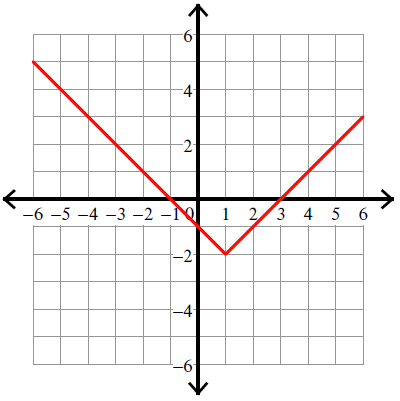
y = |x - 1| - 2
Solution :
Compare :
y = |x - h| + k
y = |x - 1| - 2
Vertex (h, k) = (1, -2).
Example 3 :
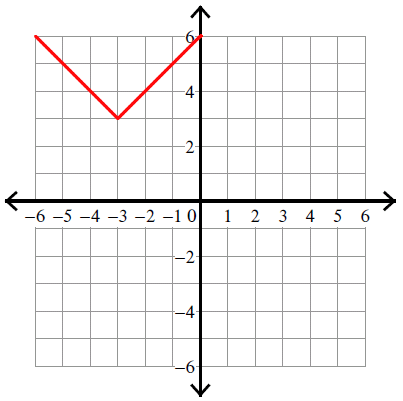
y = |x + 3| + 3
Solution :
Compare :
y = |x - h| + k
y = |x + 3| + 3
Vertex (h, k) = (-3, 3).
Example 4 :
y = |x - 2|
Solution :
y = |x - 2| ----> y = |x - 2| + 0
Compare :
y = |x - h| + k
y = |x - 2| + 0
Vertex (h, k) = (2, 0).
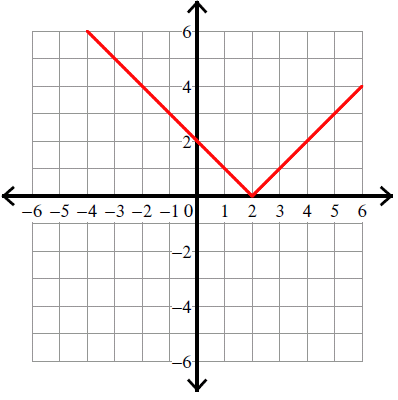
Example 5 :
y = |x + 4| + 3
Solution :
Compare :
y = |x - h| + k
y = |x + 4| + 3
Vertex (h, k) = (-4, 3).
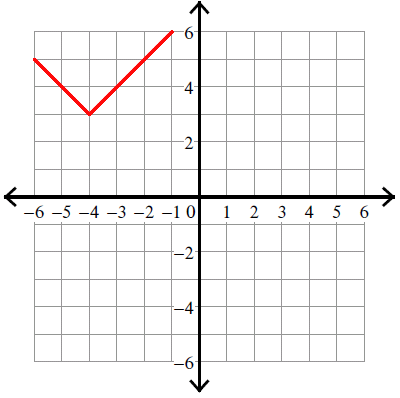
Example 6 :
y = |x - 4| - 4
Solution :
Compare :
y = |x - h| + k
y = |x - 4| - 4
Vertex (h, k) = (4, -4).
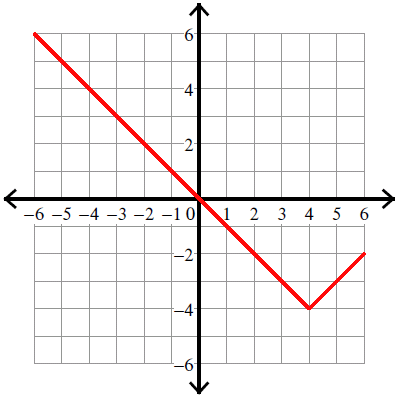
Example 7 :
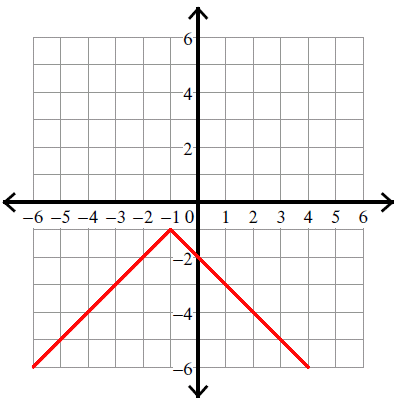
y = -|x - 2| - 2
Solution :
Compare :
y = |x - h| + k
y = -|x - 2| - 2
Vertex (h, k) = (2, -2).
Because there is negative sign in front of the absolute sign, we have to flip the curve over.
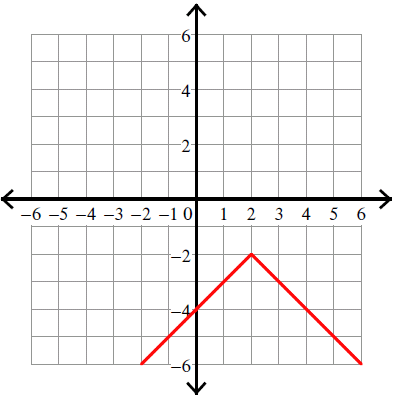
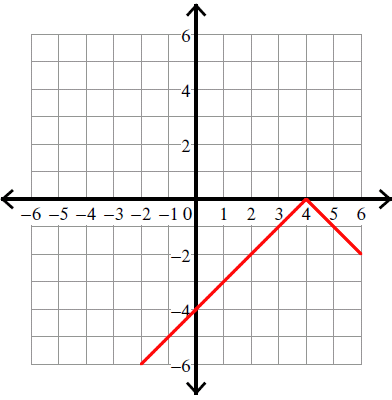
Example 8 :
y = -|x - 4|
Solution :
y = -|x - 4| ----> y = -|x - 4| + 0
Compare :
y = |x - h| + k
y = -|x - 4| + 0
Vertex (h, k) = (4, 0).
Because there is negative sign in front of the absolute sign, we have to flip the curve over.
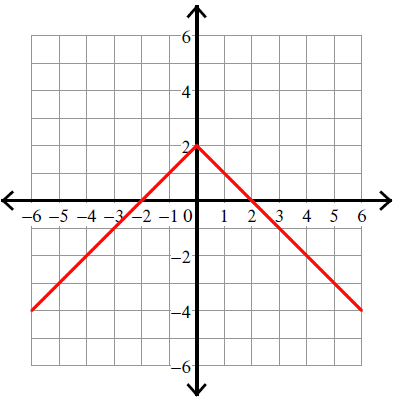
Example 9 :
y = -|x| + 2
Solution :
y = -|x| + 2 ----> y = -|x - 0| + 2
Compare :
y = |x - h| + k
y = -|x - 0| + 2
Vertex (h, k) = (0, 2).
Because there is negative sign in front of the absolute sign, we have to flip the curve over.
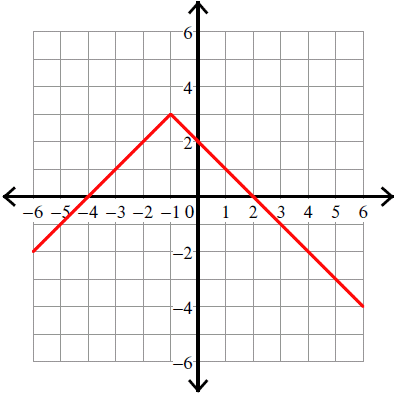
Example 10 :
y = -|x + 1| + 3
Solution :
Compare :
y = |x - h| + k
y = -|x + 1| + 3
Vertex (h, k) = (-1, 3).
Because there is negative sign in front of the absolute sign, we have to flip the curve over.
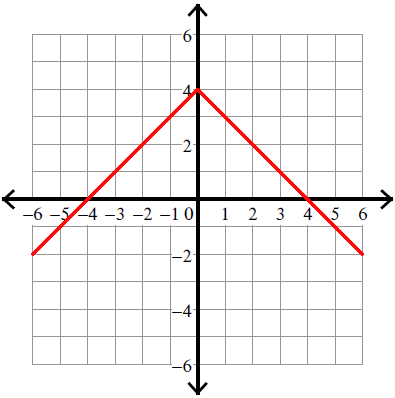
Example 11 :
y = -|x| + 4
Solution :
y = -|x| + 4 ----> y = -|x - 0| + 4
Compare :
y = |x - h| + k
y = -|x - 0| + 4
Vertex (h, k) = (0, 4).
Because there is negative sign in front of the absolute sign, we have to flip the curve over.
Example 12 :
y = -|x + 1| - 1
Solution :
Compare :
y = |x - h| + k
y = -|x + 1| - 1
Vertex (h, k) = (-1, -1).
Because there is negative sign in front of the absolute sign, we have to flip the curve over.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number

