FIND GCD OF TWO POLYNOMIALS USING DIVISION METHOD

Step 1 :

First, divide f(x) by g(x) to obtain.

f(x) = g(x)q(x)+ r(x)

where q(x) is the quotient and r(x) is remainder,

so, deg (g(x)) > deg (r(x))

If the remainder r(x) is 0, then g(x) is the GCD of f(x) and g(x).

Step 2 :

If the remainder r(x) is non-zero, divide g(x) by r(x) to obtain.

g(x) = r(x) q(x)+ r₁(x)

where r₁(x) is the remainder.

So, deg r(x) > deg r₁(x)

If the remainder r₁(x) is 0, then r(x) is the required GCD.

Step 3 :

If r₁(x) is non-zero, then continue the process until we get zero as remainder.

The remainder in the last but one step is the GCD of f(x) and g(x).

We write GCD(f(x), g(x)) to denote the GCD of the polynomials f(x) and g(x).

Example :

Find the GCD of the following pairs of polynomials using division algorithm

(i) x³-9x²+23x-15 and 4x²-16x+12

(ii) 3x³+18x²+33x+18, 3x²+13x+10

(iii) 2x³+2x²+2x+2, 6x³+12x²+6x+12

(iv) x³-3x²+4x-12, x⁴+x³+4x²+4x

(i) Answer :

x³-9x²+23x-15 and 4x²-16x+12

Let f(x) = x³-9x²+23x-15 and

g(x) = 4x²-16x+12

g(x) = 4(x²-4x+3)

Here, deg(f(x)) > deg (g(x))

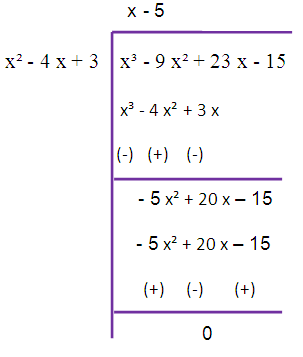
By dividing f(x) by g(x), we get 0 as remainder. So, the required GCD is x-5.

(ii) Answer :

3x³+18x²+33x+18, 3x²+13x+10

Let f(x) = 3x³+18x²+33x+18 and g(x) = 3x²+13x+10

Here, deg f(x) > deg g(x)

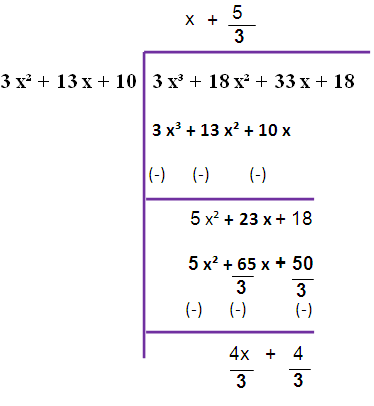
By dividing f(x) by g(x) we are not getting zero. So, we have to do this long division once again.

Now we are taking 4/3 as common from the remainder. So that we are getting (4/3)(x+1)

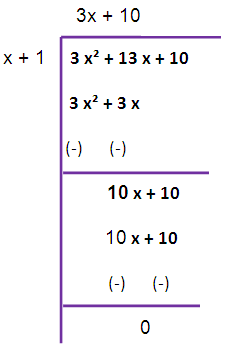
So, the greatest common divisor is x+1.

(iii) Answer :

2x³+2x²+2x+2, 6x³+12x²+6x+12

Let f(x) = 2x³+2x²+2x+2 and g(x) = 6x³+12x²+6x+12

f(x) = 2(x³+x²+x+1)

g(x) = 6(x³+2x²+x+2)

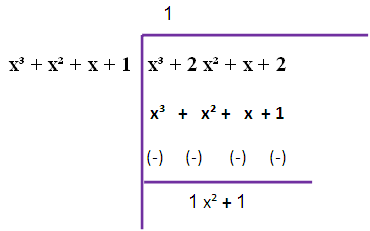
Since we are not getting zero, we have to do this long division once again

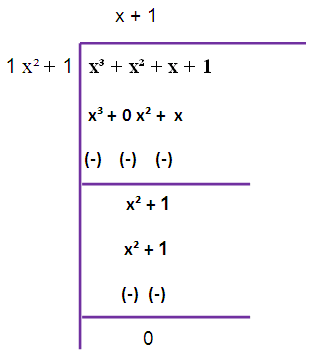
So, the required GCD is 2 (x²+1).

(vi) Answer :

x³-3x²+4x-12, x⁴+x³+4x²+4x

Let f(x) = x³-3x²+4x-12 and g(x) = x⁴+x³+4x²+4x

f(x) = x³-3x²+4x-12

g (x) = x(x³+x²+4x+4)

Here, deg (f(x)) = deg (g(x))

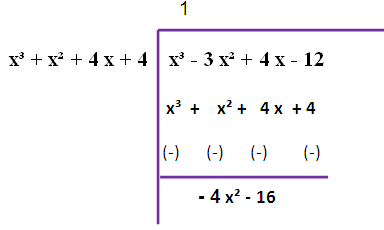
Since we are not getting zero, we have to do this long division once again

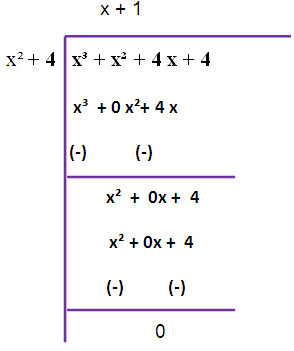
So, the required GCD is (x²+4).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

FIND GCD OF TWO POLYNOMIALS USING DIVISION METHOD

Recent Articles

Multi Step Algebra Word Problems

Solving Multi Step Word Problems Worksheet

Solving Multi Step Word Problems