FINDING THE AREA OF A RHOMBUS

The area of a rhombus is half of the product of the lengths of its diagonals.

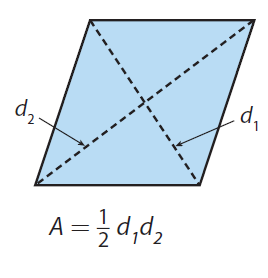
Relationship between Rhombus and Rectangle

A rhombus is a quadrilateral in which all sides are congruent and opposite sides are parallel. A rhombus can be divided into four right triangles that can then be rearranged into a rectangle.

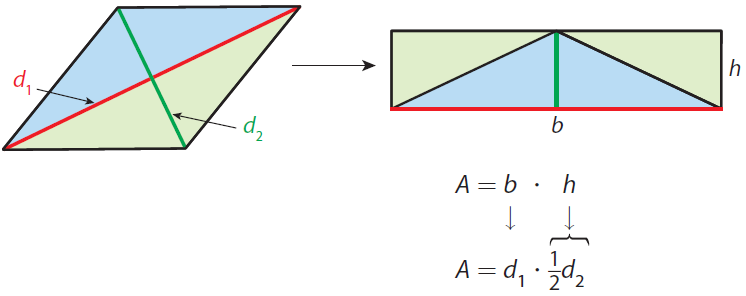
The base of the rectangle is the same length as one of the diagonals of the rhombus. The height of the rectangle is half the length of the other diagonal.

Practice Problems

Problem 1 :

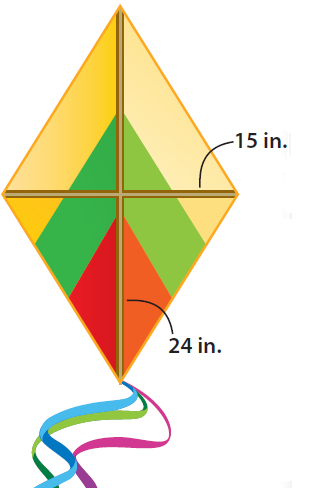
Cedric is constructing a kite in the shape of a rhombus.The spars of the kite measure 15 inches and 24 inches. How much fabric will Cedric need for the kite ?

Solution :

To determine the amount of fabric needed, find the area of the kite.

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 24 for d₁ and 15 for d₂.

=   1/2 ⋅ (24 ⋅ 15)

=   12 ⋅ 15

=  180 in²

So, Cedric needs 180 square inches of fabric to make the kite.

Problem 2 :

A kite in the shape of a rhombus has diagonals that are 25 inches long and 15 inches long. What is the area of the kite?

Solution :

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 25 for d₁ and 15 for d₂.

=   1/2 ⋅ (25 ⋅ 15)

=   1/2 ⋅ (375)

=  187.5 in²

Problem 3 :

The diagonals of a rhombus are 12 in. and 16 in. long. The length of a side of the rhombus is 10 in. What is the height of the rhombus ?

Solution :

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 12 for d₁ and 16 for d₂.

=   1/2 ⋅ (12 ⋅ 16)

=   6 ⋅ 16

=  96 in²

Because rhombus is a parallelogram, we can use the formula for area of a parallelogram to find the height of the rhombus. 

Area of parallelogram  =  96 in² 

base x height  =  96

Substitute 10 for base. 

 10 x h  =  96

Divide each side by 10. 

height  =  9.6 inches

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.