SOLVING CUBIC EQUATIONS
Every cubic equation would have 3 solutions. To solve a cubic equation, either the method factoring or synthetic division can be used.
If a cubic equation equation is factorable, factor it by grouping and solve for the variable.
Synthetic division can be used for the cubic equations which can not be factored by grouping.
Solve each of the following cubic equations.
Question 1 :
x3 + 2x2 - x - 2 = 0
Solution :
The given cubic equation can be factored by grouping.
Factor and solve.
x3 + 2x2 - x - 2 = 0
x2(x + 2) - 1(x + 2) = 0
(x + 2)(x2 - 1) = 0
|
x + 2 = 0 x = -2 |
x2 - 1 = 0 x2 - 12 = 0 (x + 1)(x - 1) = 0 x = -1 or x = 1 |
So, the solution is {-2, -1, 1}.
Question 2 :
2x3 - x2 - 4x + 2 = 0
Solution :
The given cubic equation can be factored by grouping.
Factor and solve.
2x3 - x2 - 4x + 2 = 0
x2(2x - 1) - 2(2x - 1) = 0
(2x - 1)(x2 - 2) = 0
|
2x - 1 = 0 x = 1/2 |
x2 - 2 = 0 x2 = 2 x = ±√2 |
So, the solution is {1/2, √2, -√2}.
Question 3 :
x3 - 2x2 - 5x + 6 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
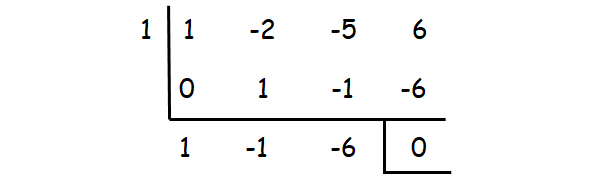
1 is one of the roots. The other roots can be determined by solving the quadratic equation
x2 - x - 6 = 0
Factor and solve.
(x - 3)(x + 2) = 0
x = 3 or x = -2
So, the solution is {1, 3, -2}.
Question 4 :
4x3 - 7x + 3 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
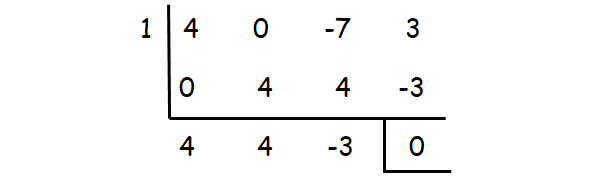
1 is one of the roots. The other roots can be determined by solving the quadratic equation
4x2 + 4x - 3 = 0
Factor and solve.
4x2 + 6x - 2x - 3 = 0
2x(2x + 3) - 1(2x + 3) = 0
(2x + 3)(2x - 1) = 0
x = -3/2 or x = 1/2
So, the solution is {1, -3/2, 1/2}.
Question 5 :
x3 - 23x2 + 142x - 120 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
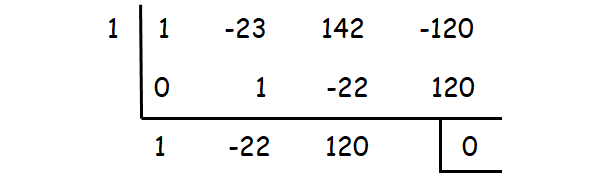
1 is one of the roots. The other roots can be determined by solving the quadratic equation
x2 - 22x + 120 = 0
Factor and solve.
(x - 10)(x - 12) = 0
x = 10 or x = 12
So, the solution is {1, 10, 12}.
Question 6 :
4x3 - 5x2 + 7x - 6 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
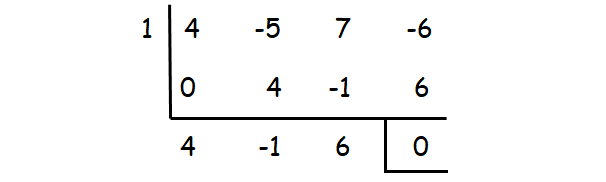
1 is one of the roots. The other roots can be determined by solving the quadratic equation
4x2 - x + 6 = 0
This quadratic equation can not be solved by factoring. So use quadratic formula and solve.
x = [-b ± √(b2 - 4ac)]/2a
a = 4, b = -1 and c = 6,
x = (1 ± √-95)/8
For the given cubic equation, there is only one real root, that is 1. The remaining two roots are imaginary.
Question 7 :
x3 - 7x + 6 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
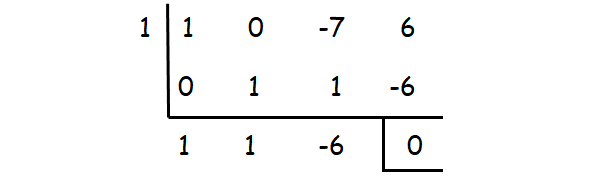
1 is one of the roots. The other roots can be determined by solving the quadratic equation
x2 + x - 6 = 0
Factor and solve.
(x + 3)(x - 2) = 0
x = -3 or x = 2
So, the solution is {1, -3, 2}.
Question 8 :
x3 + 13x2 + 32x + 20 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
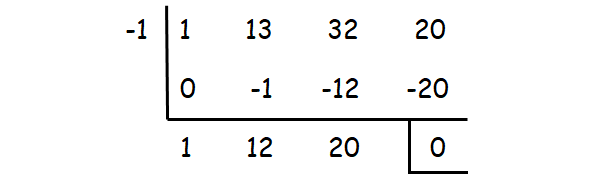
-1 is one of the roots. The other roots can be determined by solving the quadratic equation
x2 + 12x + 20 = 0
Factor and solve.
(x + 2)(x + 10) = 0
x = -2 or x = -10
So, the solution is {-1, -2, -10}.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number

