FACTORING CUBIC POLYNOMIALS
Every cubic polynomial will have 3 factors. To find those factors, we follow the following steps.
Step 1 :
We can find one linear factor of the given cubic polynomial using synthetic division.
Step 2 :
At the end of the first step, we will have quadratic factors. By factoring the quadratic equation, we can get other two factors.
Step 3 :
List all three factors.
Factor the following cubic polynomials :
Example 1 :
x3 - 2x2 - 5 x + 6
Solution :
Step 1 :
Let p(x) = x3 - 2x2 - 5 x + 6
Step 2 :
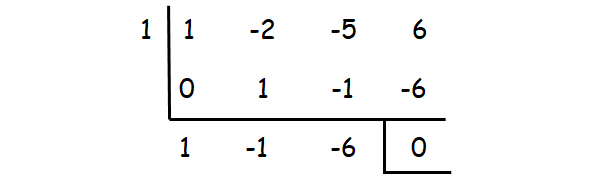
By dividing the cubic polynomial by 1, we get 0 as remainder. So (x - 1) is a factor.
We can get the other two factors, by factoring the quadratic polynomial x2 - x - 6.
x2 - x - 6 = (x - 3)(x + 2)
Step 3 :
The required factors are (x - 1) (x - 3) and (x + 2).
Example 2 :
4x3 - 7x + 3
Solution :
Step 1 :
Let p(x) = 4x3 - 7x + 3
Step 2 :
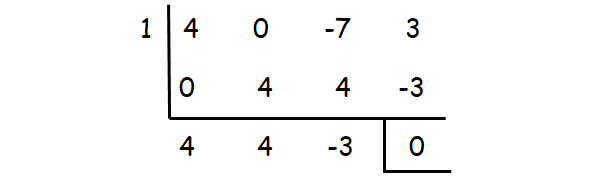
(x-1) is one of the factors.
We get the other two factors, by factoring the quadratic polynomial 4x2 + 4x -3.
= 4x2 + 6x - 2x - 3 (decomposing the middle term)
= 2x(2x + 3) - 1(2x + 3)
= (2x - 1)(2x + 3)
Step 3 :
So, the factors are (x - 1)(2x - 1)(2x + 3).
Example 3 :
x3 - 23x2 + 142x - 120
Solution :
Step 1 :
Let p(x) = x3 - 23x2 + 142x - 120
Step 2 :
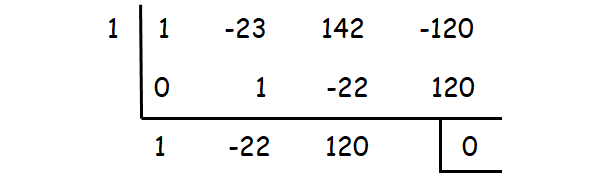
(x - 1) is a factor.
x2 - 22x + 120 = (x - 10)(x - 12)
Step 3 :
So, the factors are (x - 1)(x - 10)(x - 12).
Example 4 :
4x3 - 5x2 + 7x - 6
Solution :
Step 1 :
Let p(x) = 4x3 - 5x2 + 7x - 6
Step 2 :
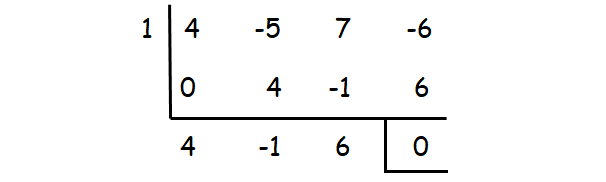
(x - 1) is one of the factors.
4x2 - x + 6 is not factorable.
Step 3 :
So, the factors are (x-1)(4x2-x+6).
Example 5 :
x3 - 7x + 6
Solution :
Step 1 :
Let p(x) = x3 - 7x + 6
Step 2 :
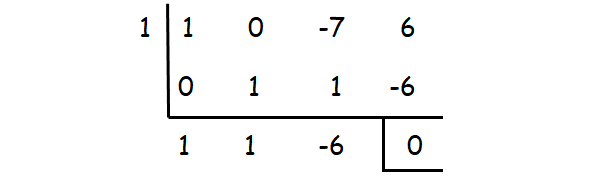
x2 + x - 6 = (x + 3)(x - 2)
Step 3 :
So, the factors are (x - 1)(x + 3)(x - 2).
Example 6 :
x3 + 13x2 + 32x + 20
Solution :
Step 1 :
Let p(x) = x3 + 13x2 + 32x + 20
Step 2 :
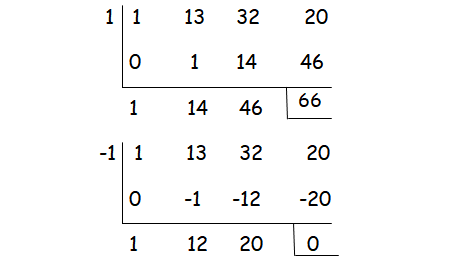
(x + 1) is one of the factors.
x2 + 12x + 20 = (x + 10)(x + 2)
Step 3 :
So, the factors are (x + 1)(x + 10)(x + 2).
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Printable Math Worksheets
Apr 20, 24 12:02 AM
Printable Math Worksheets - Worksheets in Pdf formats from grade 1 to 10 -
Printable Math Worksheets for Grade 2
Apr 19, 24 11:58 PM
Printable Math Worksheets for Grade 2 -
Sequences and Series
Apr 19, 24 11:45 PM
Sequences and Series - Concept - Examples