FIND THE EQUATION OF THE LINE WITH X AND Y INTERCEPTS

Example 1 :

Find the equation of the straight line whose x and y-intercepts on the axes are given by

(i) 2 and 3

(ii) -1/3 and 3/2

(iii)  2/5 and -3/4

Solution :

Part (i) :

To find the equation of the line whose x and y-intercepts are a and b we have to use the following  formula.

x/a + y/b = 1

Here, x -intercept (a) = 2 and y -intercept (b) = 3.

x/2 + y/3 = 1

(3x + 2y)/6 = 1

3x + 2y = 6

3x + 2y - 6 = 0

Part (ii) :

-1/3 and 3/2

Here, x-intercept (a) = -1/3 and y-intercept (b) = 3/2.

x/(-1/3) + y/(3/2) = 1

-3x + 2y/3 = 1

(-9x + 2y)/3 = 1

-9x + 2y = 3

9x - 2y + 3 = 0

Part (iii) :

2/5 and -3/4

x/a + y/b = 1

Here, x-intercept (a) = 2/5 and y -intercept (b) = -3/4.

x/(2/5) + y/(-3/4) = 1

5x/2 - 4y/3 = 1

(15x - 8y)/6 = 1

15x - 8y = 6

15x - 8y - 6 = 0

Example 2 :

Find the equation of the straight line whose x and y-intercepts on the axes are given by.

(i)

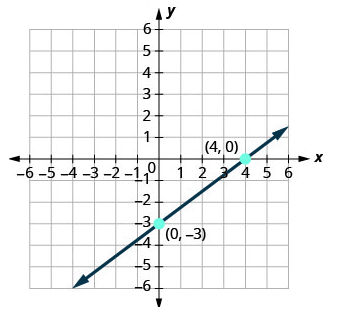
Solution :

x-intercept = 4 and y-intercept = -3

Equation of the line :

x/a + y/b = 1

x/4 + y/(-3) = 1

x/4 - y/3 = 1

(3x - 4y)/12 = 1

3x - 4y = 12

3x - 4y - 12 = 0

(ii)

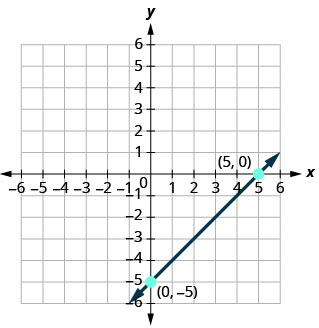
Solution :

x-intercept = 5 and y-intercept = -5

Equation of the line :

x/a + y/b = 1

x/5 + y/(-5) = 1

x/5 - y/5 = 1

(x - y)/5 = 1

x - y = 5

x - y - 5 = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.