FIND EQUATION OF THE LINE PASSING THROUGH TWO POINTS
Equation of a line using two points on the line :
(y - y1)/(y2 - y1) = (x - x1)/(x2 - x1)
Here (x1, y1) and (x2, y2) are the points on the line.
Example 1 :
Find the equation of the straight line passing through the points
(i) (-2, 5) and (3, 6)
(ii) (0, -6) and (-8, 2)
Solution :
To find equation of the line passes through two points, we use the formula given below.
(y - y1)/(y2 - y1) = (x - x1)/(x2 - x1)
(y - 5)/(6 - 5) = (x - (-2))/(3 - (-2))
(y - 5)/(1) = (x + 2)/(3 + 2)
(y - 5) = (x + 2)/5
5y - 25 = x + 2
x - 5y + 25 + 2 = 0
x - 5y + 27 = 0
(ii) (0, -6) and (-8, 2)
(y - y1)/(y2 - y1) = (x - x1)/(x2 -x1)
(y - (-6))/(2 - (-6)) = (x - 0)/(-8 - 0)
(y + 6)/(2 + 6) = -x/8
(y + 6)/8 = -x/8
y + 6 = -x
x + y + 6 = 0
Example 3 :
Find the equation of the median from the vertex R in a triangle PQR with vertices at
P (1, -3), Q (-2, 5) and R (-3, 4)
Solution :
First let us draw a rough diagram for the given information.
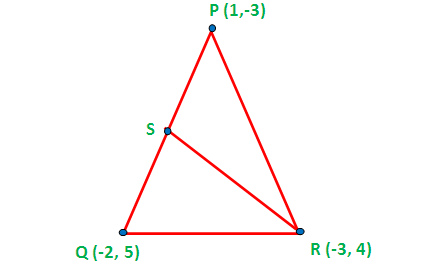
The median drawn from one vertex of the triangle will pass through the midpoint.
To find equation of the median from the vertex R, first we have to find the midpoint of the side PQ.
Midpoint = (x1 + x2)/2, (y1 + y2)/2
= (1 - 2)/2, (-3 + 5)/2
= -1/2, 2/2
= S(-1/2, 1)
Now we can use two point form to find equation of the median RS.
R(-3, 4) and S(-1/2 , 1)
(y - y1)/(y2 - y1) = (x - x1)/(x2 - x1)
(y - 4)/(1 - 4) = (x - (-1/2))/((-1/2) - (-3))
(y - 4)/(-3) = (x + (1/2))/(5/2)
(y - 4)/(-3) = (2/5)[(2x + 1)/2]
5(y - 4) = -3(2x + 1)
5y - 20 = -6x - 3
6x + 5y - 20 + 3 = 0
6x + 5y - 17 = 0
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Factoring Quadratic Trinomials Worksheet
Apr 25, 24 08:13 PM
Factoring Quadratic Trinomials Worksheet -
Factoring Quadratic Trinomials
Apr 25, 24 07:03 PM
Factoring Quadratic Trinomials - Methods - Solved Examples -
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems

