FIND EQUATION OF THE MEDIAN AND ALTITUDE WITH VERTICES

Example 1 :

If the vertices of a triangle ABC are

A (2, -4), B (3, 3) and C (-1, 5).

Find the equation of the straight line along the altitude from vertex B.

Solution :

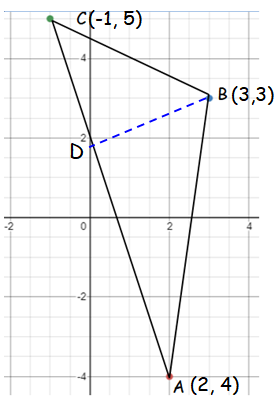
Slope of the line AC :

m  =  (y₂-y₁)/(x₂-x₁)

=  (5-(-4))/(-1-2)

=  (5+4)/(-3)

=  9/(-3)

m  =  -3  

Slope of BD  =  -1/(-3)

=  1/3

Equation of BD :

(y-y₁)  =  m(x-x₁)

(y-3)  =  (1/3)(x-3)

3(y-3)  =  1(x-3)

3y-9  =  x-3

x-3y-3+9  =  0

x-3y+6  =  0

Example 2 :

If the vertices of triangle ABC are (-4, 4) , B (8 ,4) and C (8, 10). Find the equation of the straight line along the median from A.

Solution :

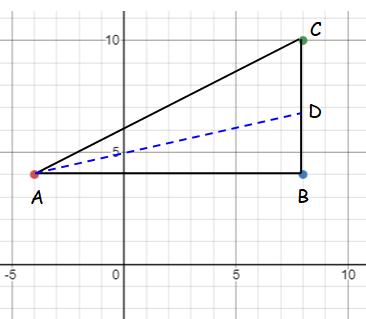
Slope of the line BC :

m  =  (y0₂-y₁)/(x₂-x₁)

=  (10-4)/(8-8)

=  6/0

m  =  0

Slope of AD  =  -1/0

Equation of AD :

(y-y₁)  =  m(x-x₁)

(y-4)  =  (-1/0)(x-(-4))

0(y-4)  =  -1(x+4)

0  =  -x-4

x+4  =  0

Example 3 :

Find the coordinates of the foot from the origin on the straight line

3x+2y  =  13.

Solution :

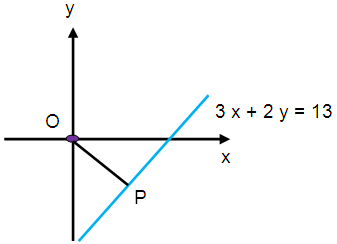
The line OP is perpendicular to the 3x+2y  =  13.

Equation of the line OP :

2x-3y+k  =  0

The line OP is passing through the origin (0 , 0)

2(0)-3(0)+k  =  0

k  =  0

So, equation of the line OP :

2x-3y+0  =  0

2x-3y  =  0

Both lines are intersecting at the point P.

3x+2y  =  13 -------- (1)

2x-3y  =  0 -------- (2)

3(1)+2(2) ==>

9x+6y+4x-6y  =  39+0

13x  =  39

x  =  3

By applying the value of x in (2), we get

2(3)-3y  =  0

6-3y  =  0

-3y  =  -6

y  =  2

So, the required point P is (3, 2).

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.