DOMAIN AND RANGE OF RATIONAL FUNCTIONS WITH HOLES
Domain of a Rational Function with Hole
Let y = f(x) be a function.
Domain of the above function is all real values of 'x' for which 'y' is defined.
If there is any value of 'x' for which 'y' is undefined, we have to exclude that particular value from the set of domain.
Let us consider the rational function given below.
y = (x2 - x - 2) / (x - 2)
In the above rational function, let us equate the denominator 'x - 2' to zero.
x - 2 = 0
x = 2
In the rational function
y = (x2 - x - 2) / (x - 2),
if x = 2, then the denominator becomes zero and the value of 'y' becomes undefined.
So, 'y' is defined for all real values of 'x' except x = 2.
Therefore, the domain is
R - {2}
Finding Hole of a Rational function
For the rational function
f(x) = (x2 - x - 2) / (x - 2),
let us try to find hole, if any.
To find hole, simplify the rational function as shown below.
In the above simplification, the common factor for numerator and denominator is (x - 2).
So there is a hole.
(Note : If there is no common factor for both numerator and denominator, then there is no hole)
Now we have to equate the common factor (x - 2) to zero.
x - 2 = 0
x = 2
So, the hole is at x = 2.
After having crossed out the common factor (x - 2), the function is simplified to
f(x) = x + 1
or
y = x + 1
Substitute x = 2.
y = 2 + 1
y = 3
So, the hole appears on the graph at (2, 3).
After simplification, the given rational function becomes
y = x + 1
which is linear and its graph will be a straight line.
Graph of 'y = x + 1'
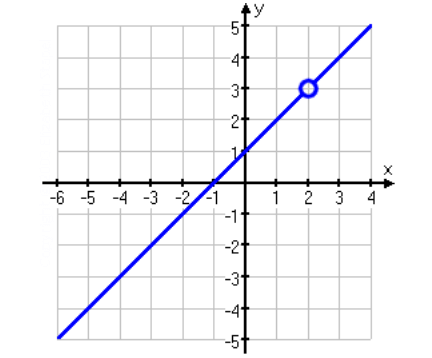
Range of a Rational Function with Hole
When we look at the above figure, the graph of
y = x + 1
appears at every real value of 'y' except at y = 3.
Because, there is a hole at
y = 3
So, the range is all real values except '3'.
That is,
R - {3}
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
Recent Articles
-
Addition Word Problems
Jul 13, 20 10:38 PM
Addition Word Problems
-
Addition Word Problems Worksheet
Jul 13, 20 10:28 PM
Addition Word Problems Worksheet
-
ACT Math Practice Test Online
Jul 12, 20 01:14 AM
ACT Math Practice Test Online
