DISJOINT SETS
Disjoint is one of the important operations on sets.
Let us discuss this operation in detail.
Two sets X and Y are said to be disjoint if they do not have any common element. That is, X and Y are disjoint if
X n Y = Empty set
It is clear that n(A u B) = n(A) + n(B), if A and B are disjoint finite set.
The Venn diagram given below illustrates the two disjoint sets X and Y.
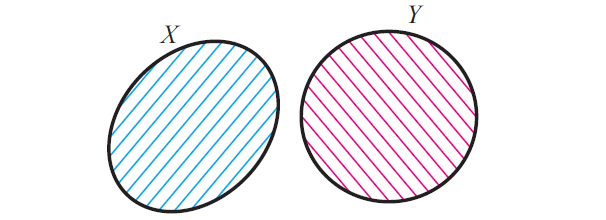
Example 1 :
Let A = {1, 3, 5, 6}, B = {0, 7}, find A n B.
Solution :
A n B = {1, 3, 5, 6} u {0, 7}
A u B = { } or empty set
Hence, A and B are disjoint sets.
Example 2 :
Let A = {0, 2, 7, 9}, B = {1, 3, 4, 7}, find A Δ B. When A and B are disjoint sets, verify A Δ B = A u B.
Solution :
A\B = A - B
= {0, 2, 7, 9} - {1, 3, 4, 7}
= {0, 2, 7, 9}
B\A = B - A
= {1, 3, 4, 7} - {0, 2, 7, 9}
= {1, 3, 4, 7}
A Δ B = (A\B) u (B\A)
A Δ B = {0, 2, 7, 9} u {1, 3, 4, 7}
A Δ B = {0, 2, 7, 9, 1, 3, 4, 7} ----(1)
A n B = {0, 2, 7, 9} n {1, 3, 4, 7}
A n B = { } ----(2)
A and B are disjoint sets.
A u B = {0, 2, 7, 9} u {1, 3, 4, 7}
A u B = {0, 2, 7, 9, 1, 3, 4, 7} ----(2)
From (1), (2) and (3), it is clear that if A are B disjoint sets, then
A Δ B = A u B
Related Pages
4. Symmetric difference of two sets
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number
