DILATION TRANSFORMATION MATRIX
Dilation transformation matrix is the matrix which can be used to make dilation transformation of a figure.
Dilation - Definition
A dilation is a transformation that produces an image that is the same shape as the original, but is a different size. NOT an isometry. Forms similar figures.
In simple words, dilation means, it just re sizes the given figure without rotating or anything else.
Dilation Rule Using Matrix
Let A ( -2, 1), B (2, 4) and (4, 2) be the three vertices of a triangle. First we have to write the given vertices in matrix form as given below.
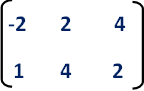
If the given figure is dilated by the scale factor "k", then the dilation transformation matrix would be as given below.
Vertices of the translated image are
(-2k, k), (2k, 4k), (4k, 2k)
Dilation for "k = 2"
Once students understand the above mentioned rule which they have to apply for dilation transformation, they can easily make dilation-transformation of a figure.
For example, if we are going to make dilation transformation of the point (5, 3) for the scale factor "k = 2" , after transformation, the point would be (10, 6).
Here, the rule we have applied is
(x, y) -------> (kx, ky)
For k = 2, we get
(5, 3) -------> (10, 6)
Let us consider the following example to have better understanding of dilation.
Question :
Let A(-2, 1), B(2, 4) and C(4 , 2) be the three vertices of a triangle. If this triangle is dilated by the scale factor "k = 2", what will be the new vertices A', B' and C' ?
Solution :
Step 1 :
First we have to write the vertices of the given triangle ABC in matrix form as given below.
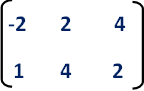
Step 2 :
Here, triangle is dilated by the scale factor "k = 2". So each element of the above matrix to be multiplied by 2.
When we do so, the matrix we get
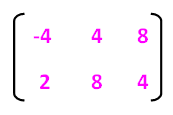
Step 3 :
From the matrix in step 2, we can get the vertices of the dilated triangle for the scale factor k = 2.
Vertices of the dilated triangle are
A'(-4, 2) , B'(4, 8) and C'(8, 4)
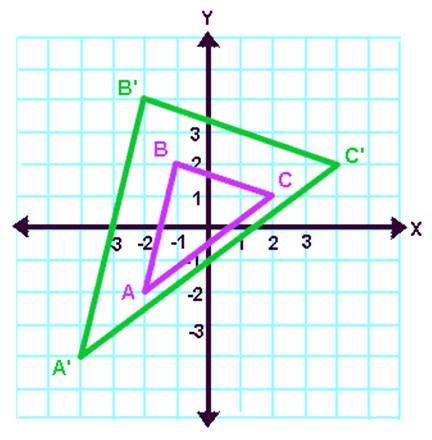
How to sketch the dilated figure?
1. First we have to plot the vertices of the pre-image.
2. In the above problem, the vertices of the pre-image are
A(-2, 1), B(2, 4) and C(4, 2)
3. When we plot these points on a graph paper, we will get the figure of the pre-image (original figure).
4. When we dilate the given figure for "k = 2", we have to apply the formula
(x, y) -------> (kx, ky)
5. When we apply the formula, we will get the following vertices of the image (dilated figure).
6. In the above problem, vertices of the image are
A'(-4, 2), B'(4, 8) and C'(8, 4)
7. When plot these points on the graph paper, we will get the figure of the image (dilated figure).
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Model Polynomial Multiplication
Oct 25, 20 05:39 AM
Model Polynomial Multiplication
-
Properties of Quadratic Equations
Oct 25, 20 03:45 AM
Properties of Quadratic Equations
-
Properties of Equality
Oct 25, 20 03:22 AM
Properties of Equality - Concept - Solved Problems
