DIFFERENT FORMS OF EQUATION OF STRAIGHT LINE
Suppose that we have the graph of a straight line and we want to find its equation.
For any straight line, if we want to find the equation, we must have the following information of that straight line.
1. Slope and y-intercept
2. One point and slope
3. Two points
4. x-intercept and y-intercept
If we have any one of the five information above, we can find the equation of a line using the formulas given below.
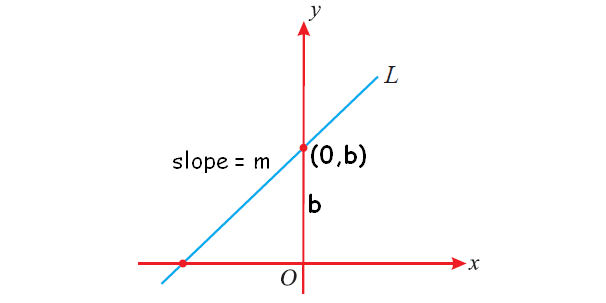
1. Slope-Intercept form equation of a line :
y = mx + b
m ---> slope
b ----> y-intercept
2. Point-Slope form equation of a line :
y - y1 = m(x - x1)
m ---> slope
(x1, y1) ----> point
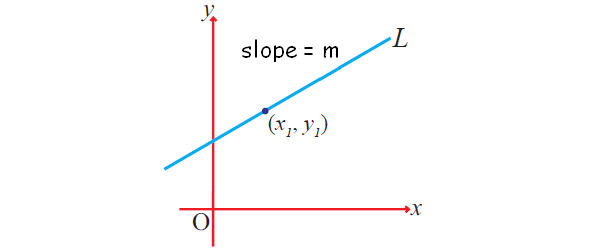
3. Two-Points form equation of a line :
Two points ----> (x1, y1) and (x2, y2)
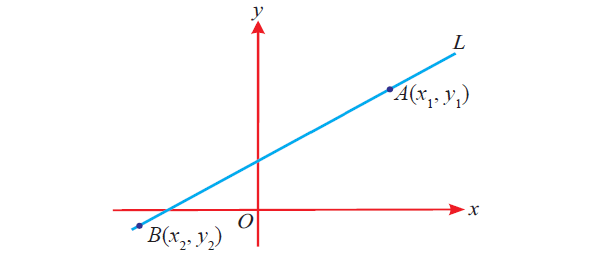
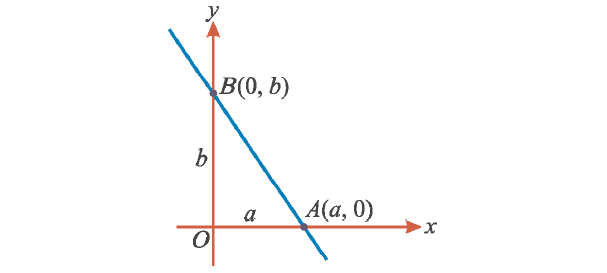
4. Intercept-Form equation of a line :
a ----> x-intercept
b ----> y-intercept
Apart from the above forms of equation of straight line, there are some other ways to get equation of a straight line.
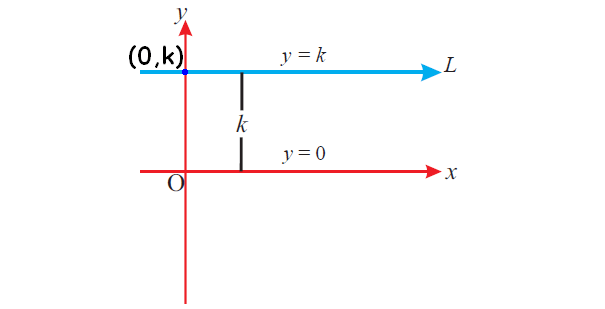
1. If a straight line is passing through a point (0, k) on y-axis and parallel to x-axis, then the equation of the straight line is y = k.
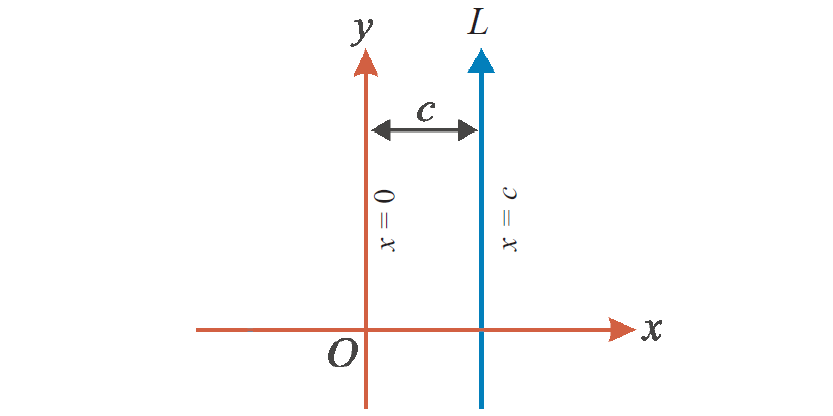
2. If a straight line is passing through a point (c, 0) on x-axis and parallel to y-axis, then the equation of the straight line is x = c.
3. Equation of x-axis :
y = 0
(Because, the value of y in all the points on x-axis is zero)
4. Equation of y-axis :
x = 0
(Because, the value of x in all the points on y-axis is zero)
5. Equation of a line in general form :
ax + by + c = 0
6. Equation of a line in standard form :
ax + by = c
Solved Problems
Problem 1 :
Find the equations of the straight lines parallel to the coordinate axes and passing through the point (3, -4).
Solution :
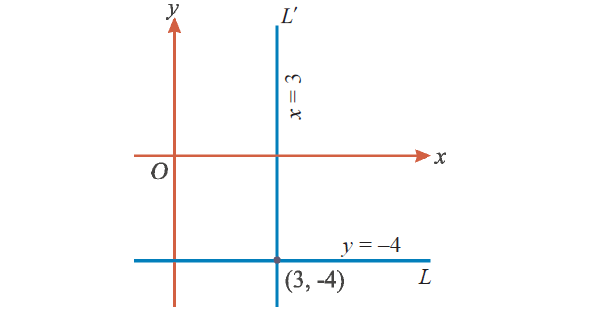
Let L and L' be the straight lines passing through the point (3, -4) and parallel to x-axis and y-axis respectively.
The y-coordinate of every point on the line L is – 4.
Hence, the equation of the line L is
y = -4
Similarly, the x-coordinate of every point on the straight line L' is 3.
So, the equation of the line L' is
x = 3
Problem 2 :
Find the general equation of the straight line whose angle of inclination is 45° and y-intercept is 2/5.
Solution :
From the angle of inclination 45°, we can get the slope.
Slope of the line :
m = tan45°
m = 1
Given : y-intercept b = 2/5.
Equation of a straight line in slope-intercept form :
y = mx + b
Substitute m = 1 and b = 2/5.
y = x + 2/5
Multiply each side by 5.
5y = 5x + 2
Subtract 5y from each side.
0 = 5x - 5y + 2
5x - 5y + 2 = 0
Problem 3 :
Find the general equation of the straight line passing through the point (-2, 3) with slope 1/3.
Solution :
Given : Point = (-2, 3) and slope m = 1/3.
Equation of a straight line in point-slope form :
y - y1 = m(x - x1)
Substitute (x1 , y1) = (-2 , 3) and m = 1/3.
y - 3 = (1/3)(x + 2)
Multiply each side by 3.
3(y - 3) = x + 2
Simplify.
3y - 9 = x + 2
Subtract 3y from each side.
-9 = x - 3y + 2
Add 9 to each side.
0 = x - 3y + 11
x - 3y + 11 = 0
Problem 4 :
Find the equation of a straight line in slope intercept form which is passing through the points (-1, 1) and (2, -4).
Solution :
Given : Two points on the straight line : (-1, 1) and (2, -4).
Equation of a straight line in two-points form :
y - y1 = [(y2 - y1)/(x2 - x1)](x - x1)
Substitute (x1 , y1) = (-1, 1) and (x2, y2) = (2, -4).
y - 1 = [(-4 - 1)/(2 + 1)](x + 1)
y - 1 = (-5/3)(x + 1)
y - 1 = -5x/3 - 5/3
y = -5x/3 - 5/3 + 1
y = -5x/3 - 2/3
Problem 5 :
The vertices of a triangle ABC are A(2, 1), B(-2, 3) and C(4, 5). Find the equation of the median through the vertex A.
Solution :
Median is a straight line joining a vertex and the midpoint of the opposite side.
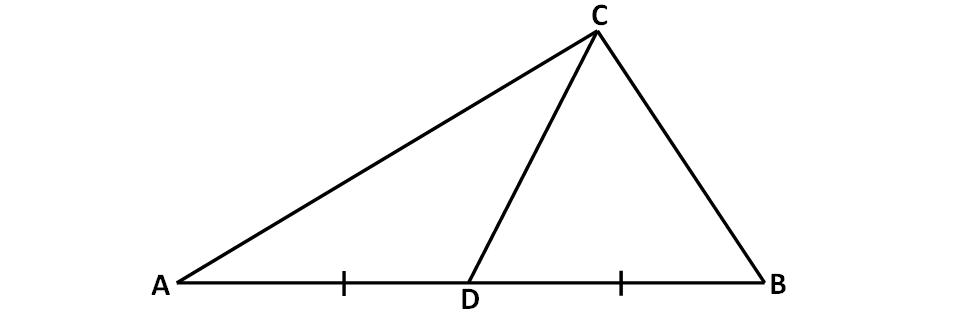
In ΔABC above, midpoint of BC :
= D((-2 + 4)/2, (3 + 5)/2)
= D(1, 4)
The median through A is the line joining two points A (2, 1) and D(1, 4).
Equation of the median through A :
(y - y1)/(y2 - y1) = (x - x1)/(x2 - x1)
Substitute (x1 , y1) = (2, 1) and (x2, y2) = (1, 4).
(y - 1)/(4 - 1) = (x - 2)/(1 - 2)
(y - 1)/3 = (x - 2)/(-1)
-1(y - 1) = 3(x - 1)
-y + 1 = 3x - 3
3x + y - 4 = 0
Problem 6 :
If the x-intercept and y-intercept of a straight line are 2/3 and 3/4 respectively, find the general equation of the straight line.
Solution :
Given : x- intercept is 2/3 and y-intercept is 3/4.
Equation of a straight line in intercept form :
x/a + y/b = 1
Substitute a = 2/3 and b = 3/4.
x/(2/3) + y/(3/4) = 1
3x/2 + 4y/3 = 1
(9x + 8y)/6 = 1
Multiply each side by 6.
9x + 8y = 6
Subtract 6 from each side from 6.
9x + 8y - 6 = 0
Problem 7 :
Find the equations of the straight lines each passing through the point (6, -2) and whose sum of the intercepts is 5.
Solution :
Let 'a' and 'b' be the x-intercept and y-intercept of the required straight line respectively.
Given : Sum of the intercepts is 5.
a + b = 5
Subtract 'a' from each side.
b = 5 - a
Equation of a straight line in intercept form :
x/a + y/b = 1
Substitute b = 5 - a.
x/a + y/(5 - a) = 1
[(5 - a)x + ay]/a(5-a) = 1
(5 - a)x + ay = a(5 - a) ----(1)
The line is passing through (6, -2).
So, substitute (x, y) = (6, -2).
(5 - a)6 - 2a = a(5 - a)
30 - 6a - 2a = 5a - a2
a2 - 13a + 30 = 0
a2 - 13a + 30 = 0
(a - 10)(a - 3) = 0
a = 10 and a = 3
When a = 10,
(1)----> (5 - 10)x + 10y = 10(5 - 10)
-5x + 10y = -50
5x - 10y - 50 = 0
x - 2y - 10 = 0
When a = 3,
(1)---->(5 - 3)x + 3y = 3(5 - 3)
2x + 3y = 6
Problem 8 :
Find the general equations of the straight lines parallel to x- axis which are at a distance of 5 units from the x-axis.
Solution :
From the given information, we can sketch the two lines as shown below.
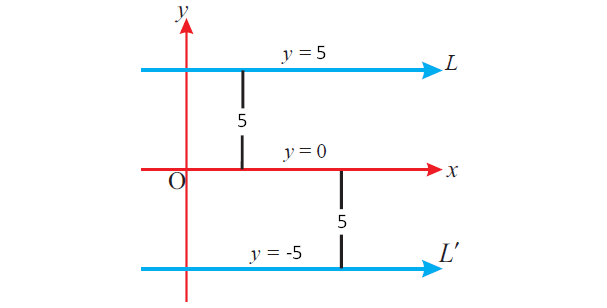
One line is above the x-axis at a distance of 5 units. And another line is below the x-axis at a distance of 5 units.
So, y = 5 and y = -5 are the required straight lines.
Problem 9 :
Find the slope and y-intercept of the straight line whose equation is 4x - 2y + 1 = 0.
Solution :
Since we want to find the slope and y-intercept, let us write the given equation 4x - 2y + 1 = 0 in slope-intercept form.
4x - 2y + 1 = 0
4x + 1 = 2y
(4x + 1)/2 = y
2x + 1/2 = y
y = 2x + 1/2
The above form is in slope intercept form.
Comparing y = 2x + 1/2 and y = mx + b,
m = 2 and b = 1/2
Problem 10 :
A straight line has the slope 5. If the line cuts y-axis at -2, find the general equation of the straight line.
Solution :
Since the line cuts y-axis at -2, clearly y-intercept is -2.
So, the slope m = 5 and y-intercept b = -2.
Equation of a straight line in slope-intercept form :
y = mx + b
Substitute m = 5 and b = -2.
y = 5x - 2
Subtract y from each side.
5x - y - 2 = 0
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet -
Factoring Quadratic Trinomials Worksheet
Apr 25, 24 08:13 PM
Factoring Quadratic Trinomials Worksheet
