DEFINE INTEGRALS
Example 1 :
Evaluate the following
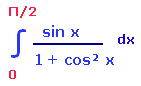
Solution :
Let t = cos x
Differentiating both sides with respect to x
dt = -sin x dx and sin x dx = -dt
We have changed the given function in terms of t from the variable x .So, we need to change the limits also.
|
When x = 0 t = cos 0 t = 1 |
When x = Π/2 t = cos Π/2 t = 0 |

Example 2 :
Evaluate the following
Integral 0 to Π/2 sin² x
Solution :
To solve this problem we have to use the trigonometric formula for sin² x.
sin²x = (1 - cos 2x)/2
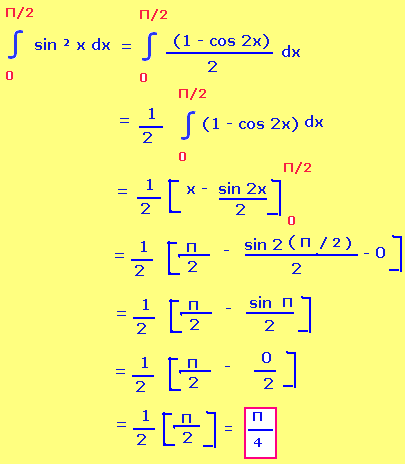
Example 3 :
Evaluate the following
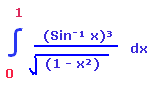
Solution :
t = Sin⁻¹x
Differentiating with respect to x on both sides
dt = 1/√(1-x²) dx
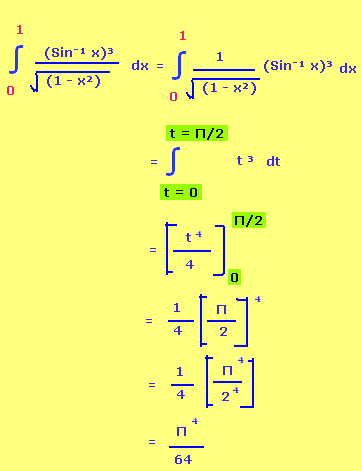
Related Pages
- Integration
- Example problems using he above formulas
- Substitution method
- Decomposition method
- Properties of integrals
- Integration-by parts
- Integration-of Sec³x
- Standard integrals
- Integrating quadratic denominator
- Integration-using partial fractions

Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems -
Converting Between Polar and Rectangular Coordinates
Apr 23, 24 11:08 AM
Converting Between Polar and Rectangular Coordinates

