CURVED SURFACE AREA

Curved surface area of a solid is the measurement of outer area,where the extension of top and bottom portion wont be included. 

Curved surface area of cylinder:

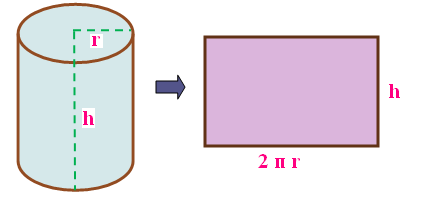
If a rectangle revolves about one side and completes one full rotation, the solid thus formed is called a right circular cylinder. The above picture shows that how rectangle forms a right circular cylinder. In other words curved surface area can be simply said as CSA.

CSA of cylinder = 2 π r h

"r" and "h" stands for radius and height of cylinder.

Curved surface area of Sphere:

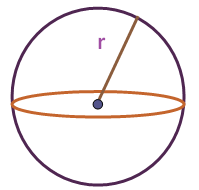
If we consider the shapes like sphere, both total surface area and CSA would be same.

Because in the shape sphere, we don't need any specific top portion or bottom portion (circles or any other shapes) as we have for cylinder

CSA of sphere = 4 π r²

Here "r" represents radius of the sphere.

Curved surface area of hemisphere:

CSA of hemisphere = 4 π r²

Curved surface area of Cone:

And for the shapes like cone, we don't have any specific shape at the top portion. But we have the circle at the base (bottom). So when we want to find the CSA of a cone, we need to find the area that exclude the extension of the bottom portion or base.In the top portion.

We don't need to exclude anything. Because there will be only one vertex at the top.So we don't have to exclude any thing at the top when we want to find CSA of cone.

CSA of cone = π r l 

Here "r" represents radius and "L" represents slant height of the cone.

Example problems of CSA :

Question 1

A solid right circular cylinder has radius of 14 cm and height of 8 cm. Find its CSA

Solution:

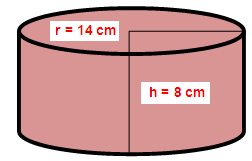
Radius of the cylinder (r) = 14 cm

Height of the cylinder (h) = 8 cm

CSA of cylinder  =  2 Π r h

=  2 x (22/7) x 14 x 8

=  704 sq.cm

CSA of cylinder = 704 sq.cm

Hence, CSA of cylinder is 704 sq.cm

Question 2:

Curved surface area and circumference at the base of a solid right circular cylinder are 4400 sq.cm and 110 cm respectively. Find its height and diameter.

Solution:

CSA of cylinder = 4400 sq.cm

Circumference of the base = 110 cm

2 Π r  =   110 ==> 2 x (22/7) x r  =  110

r  =  110 x (1/2) x (7/22)  ==> r  =  17.5 cm

diameter  =  2 r

=  2 (17.5) ==> 35 cm 

2 Π r h   =   4400 ==> 110 x  h  =  4400 ==> h  =  4400/110

h  =  40 cm 

Height = 40 cm

Diameter of the cylinder = 35 cm

Question 3:

A mansion has 12 right cylindrical pillars each having radius 50 cm and height 3.5 m. Find the cost to paint the lateral surface of pillars at $ 20 per square meter.

Solution:

The pillars of the mansion are in the shape of cylinder 

Radius = 50 cm ==>  0.5 m

Height = 3.5 m

CSA of one pillar = 2 x (22/7) x 0.5 x 3.5

=  2 x 22 x 0.5 x 0.5 ==> 11 m²

CSA of 12 pillars = 12 x 11 ==> 132 m²

Cost to paint per m² = $ 20

Total cost = 20 x 132

=  $ 2640   

Hence, total cost of painting 12 pillars is $ 2640

Question 4:

If the circumference of the base of the solid right circular cone is 236 and its slant height is 12 cm, find its CSA.

Solution:

Circumference of the base = 236 cm

Slant height (L) = 12 cm

2 Π r = 236 ==> Π r = 236/2 ==> 118

CSA of cone = Π r l

= 118 (12) ==>  1416 cm² 

CSA of cone = 1416 cm² 

Question 5:

A heap of paddy is in the form of a cone whose diameter is 4.2 m and height is 2.8 m. If the heap is to be covered exactly by a canvas to protect it from rain,then find the area of the canvas needed.

Solution:

Diameter of heap of paddy = 4.2 m

r = 4.2/2 ==> 2.1 m

height of paddy (h) = 2.8 m

L² = r²  + h²

L =  √(2.1)² + (2.8)² ==> √4.41 + 7.84 ==>√12.25 = 3.5 

CSA of heap of paddy = Π r l

 = (22/7) x (2.1) x (3.5) ==> 22 x (2.1) x (0.5) ==> 23.1 cm²

CSA of paddy = 23.1 cm²

Question 6:

The central angle and radius of a sector of a circular disc are 180 degree and 21 cm respectively. If the edges of the sector are joined together to make a hollow cone,then find the radius of the cone.

Solution:

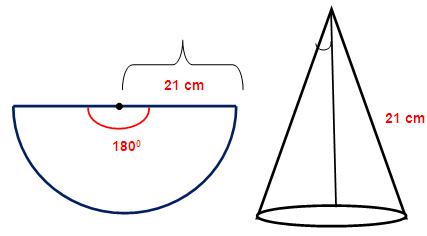
The cone is being created by joining the radius. So the radius of the sector is going to be the slant height of the cone.

 Slant height (L) = 21 cm

 Arc length of the sector = Circumference of the base of the cone

 Length of arc = (θ/360) x 2Π R

Here R represents radius of the sector

= (180/360) x 2 x (22/7)x (21) ==> (1/2) x 2 x 22x 3 ==>  66 cm

 So,circumference of the base of the cone = 66

 2 Π r =  66 ==> 2 x (22/7) x r = 66 ==> r = 10.5 cm

Radius of the cone = 10.5 cm

Question 7 :

If the curved surface area of solid sphere is 98.56 cm², then find the radius of the sphere.

Solution:

CSA of sphere = 98.56 cm²

4 Π r²  = 98.56 ==> 4 x (22/7) x r²  = 98.56

r²  = 98.56 x (1/4) x (7/22) ==> r²  = 7.84 ==> 2.8 cm

Radius of the sphere = 2.8 cm

Question 8 :

If the curved surface area of the solid hemisphere is 2772 sq.cm, then find its radius.

Solution:

Curved surface area of hemisphere = 2772 cm²

 2 Π r²  = 2772 ==> 2 x (22/7) x r²  = 2772

r²  = 2772  x (1/2) x (7/22) ==> r²  = 441 ==>  r = 21

Radius of hemisphere = 21 cm

Question 9 :

Radii of two solid hemispheres are in the ratio 3:5. Find the ratio of their curved surface areas

Let r₁ and r₂ are the radii of two hemispheres

r₁ : r₂ = 3 : 5

r₁/ r₂ = 3/5

r₁= 3 r₂/5

Curved surface area of hemisphere =  2 Π r²

Ratio of CSA of two hemisphere

2 Π r₁² : 2 Π r₂²

(3 r₂/5)² : r₂²  ==> 3²/5² : 1 ==>  9 : 25

Ratio of CSA is 9 : 25

Question 10 :

Find the CSA of a hollow hemisphere whose outer and inner radii are 4.2 cm and 2.1 cm respectively.

Solution:

Inner radius (r) = 2.1 cm

Outer radius (R) = 4.2 cm

CSA of hollow hemisphere = 2Π (R² + r²) 

= 2 x Π x [(4.2)² + (2.1)²] ==> 2 x Π x (17.64 + 4.41)

= 2 x Π x (22.05) ==>  44.1 Π cm²

CSA of hollow hemisphere = 44.1 Π cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.