PROBLEMS ON SURFACE AREA OF CYLINDER
Curved surface area of cylinder is the measurement of outer area, where the extension of top and bottom portion wont be included.
Curved surface area of cylinder
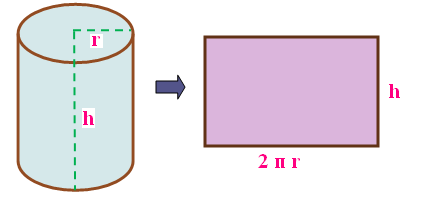
If a rectangle revolves about one side and completes one full rotation, the solid thus formed is called a right circular cylinder. The above picture shows that how rectangle forms a right circular cylinder. In other words curved surface area is simply said as CSA
CSA of cylinder = 2 π r h
"r" and "h" stands for radius and height of cylinder.
Curved surface area of hollow cylinder
A hollow cylinder is a three dimensional solid bounded by two parallel cylindrical surfaces and by two parallel circular bases cut out from two parallel planes by these two cylindrical surfaces.
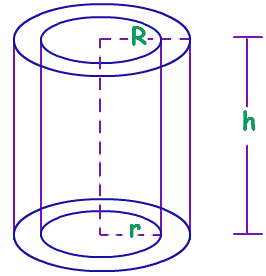
CSA of hollow cylinder = 2πh(R+r)
R = external radius, r = internal radius and h = height
Example 1 :
The external surface area of a hollow cylinder is 540Π cm2.Its internal diameter is 16 cm and height is 15 cm. Find the curved surface area.
Solution :
External surface area of cylinder = 540 Π cm²
2 Π R h = 540 Π cm²
Internal radius (r) = 16/2 = 8 cm
height (h) = 15 cm
2⋅ Π ⋅ R ⋅ h = 540 Π
2 Π R⋅15 = 540 Π
= 540 Π ⋅ (1/2) ⋅ (1/Π) ⋅ (1/15)
= 270/(15)
R = 18
Curved surface area = 2 Π h (R + r)
= 2Π(15)(18+8)
= 390Π cm2
Curved surface area of the cylinder = 390Π cm2
Example 2 :
The external diameter of the cylindrical shaped iron pipe is 25 cm and its length is 20 cm. If the thickness of the pipe is 1 cm, find the curved surface area of the pipe.
Solution :
External radius of the pipe (R) = 12.5 cm
height of the pipe (h) = 20 cm
thickness of the pipe (w) = 1 cm
To find curved surface area of the cylinder, we have to find the internal radius (r)
W = R - r
1 = 12.5 - r
r = 12.5 - 1
r = 11 .5 cm
Curved surface area = 2 Π h (R + r)
= 2 Π (20) (12.5 + 11.5)
= 960 Π cm2
Hence curved surface area of cylinder is 960 Π cm2.
Example 3 :
The radii of two right circular cylinders are in the ratio 3:2 and their heights are in the ratio 5:3. Find the ratio of their curved surface areas.
Solution :
Let r1 , r2 and h1, h2 are radii and heights of first and second cylinders respectively.
Now we have to find the ratio of their curved surface areas
Curved surface area of cylinder = 2Πrh
Curved surface area of first cylinder = 2Πr1h1
Curved surface area of second cylinder = 2Πr2h2
r1 : r2 = 3:2
r1/r2 = 3/2
r1 = 3r2/2
h1 : h2 = 5 : 3
h1/h2 = 5/3
h1 = 5h2/3
Ratios of curved surface area of two cylinders
2Πr1h1 : 2Πr2h2
(3r2/2) (5h2/3) : r2 : h2
= 5/2 : 1
= 5 : 2
So, ratio of their curved surface areas is 5 : 2.
Example 4 :
The diameter of the road roller of length 120 cm is 84 cm. If it takes 500 complete revolutions to level play ground, then find the cost of leveling it at the cost of $ 1.5 per square meter.
Solution :
Radius of cylinder (r) = 84/2
r = 42 cm
height of cylinder (h) = 120 cm
Area covered by road roller in one revolution = CSA of the road roller
Curved surface area of cylinder = 2 Π r h
= 2 ⋅ (22/7) ⋅ 42 ⋅ 120
= 31680 cm2
Area covered by 500 revolutions = 500 x 31680
= 15840000 cm2
= 1584 m2
Cost of leveling per square meter = $1.5
Required cost = 1584 x 1.5
= $2376
So, required cost is $ 2376.
Example 5 :
The internal and external radii of of a hollow cylinder are 12 cm and 18 cm respectively. If its height is 14 cm, then find its curved surface area.
Solution :
External radius (R) = 18 cm
Internal radius (r) = 12 cm
height (h) = 14 cm
Curved surface area = 2Πh (R+r)
= 2 ⋅ (22/7) (14) (18 + 12)
= 2640 cm2
So, curved surface area of cylinder is 2640 cm2

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
