CONVERTING WITHIN MEASUREMENT SYSTEMS

The two most common systems of measurement are the customary system and the metric system.

If we do conversion within customary system or metric system, it is called converting units within measurement systems. 

That is, we are not doing conversion of units from customary to metric or metric to customary. 

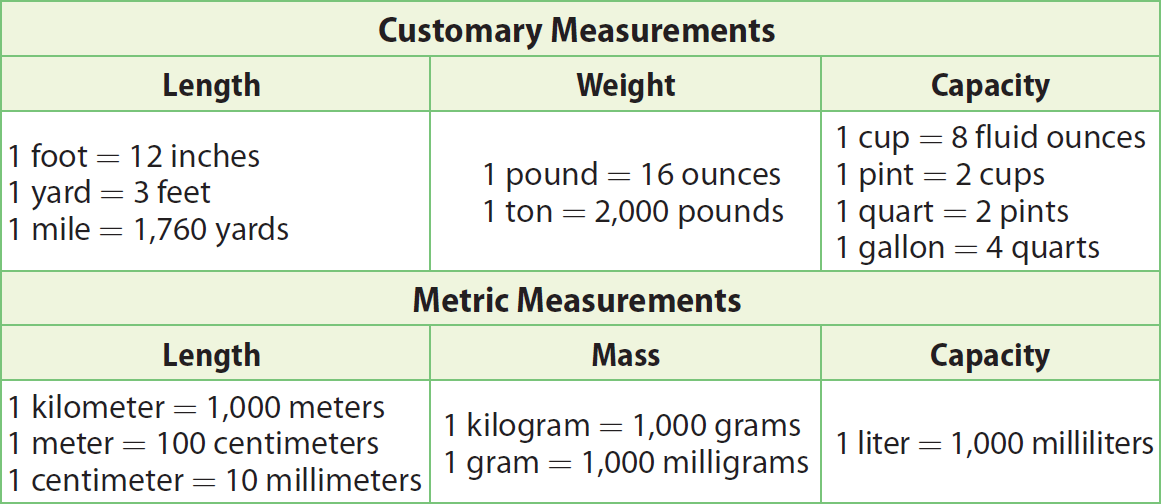
The table given below is much useful to do  conversion of units within customary and metric systems. 

Using a Model to Convert Units

Question :

Use a model to do the following conversion. 

Convert 12 feet into yards

Convert 18 yards into feet

Solution : 

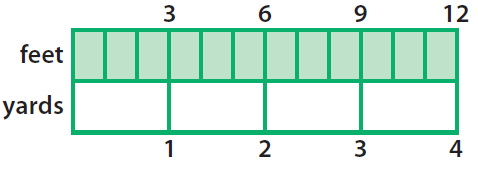
Let us write ratios of feet to yards from the above model. 

3/1,  6/2,  9/3,  12/4

From the above equivalent ratios, it is clear that for an increase of every yard, there is an increment of 3 feet. 

So, the ratio of feet to yards in any measurement from the above model is

3 feet / 1 yard

To convert 12 feet into yards,  we have to change the first quantity in the above ratio as 12 using multiplication. 

3 / 1  =  (3x4) / (1x4)  =  12 feet / 4 yards

Therefore, 12 feet  =  4 yards.

To convert 12 feet into yards,  we have to change the second quantity of the ratio 3/1 as 18 using multiplication. 

3 / 1  =  (3x18) / (1x18)  =  54 feet / 18 yards

Therefore, 18 yards  =  54 feet.

Solved Examples

Example 1 :

Convert 3.5 yards into inches. 

Solution : 

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 yards  =  3.5 x 36 inches

3.5 yards  =  126 inches

Example 2 :

Convert 3.5 tons into pounds  . 

Solution : 

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 tons  =  3.5 x 2000 pounds

3.5 tons  =  7000 pounds

Example 3 :

Convert 24 quarts into gallons 

Solution : 

Here, we convert smaller unit into bigger unit. So we have to divide.

24 quarts  =  24 / 4 gallons 

24 quarts  =  6 gallons 

Example 4 :

Convert 3.5 decimeters into centimeters. 

Solution : 

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 dm  =  3.5 x 10 cm

3.5 dm  =  35 cm

Example 5 :

Convert 48 milligrams into centigrams. 

Solution : 

Here, we convert smaller unit into bigger unit. So we have to divide.

48 milligrams  =  48 / 10 centigrams 

48 milligrams  =  4.8 centigrams

Example 6 :

Convert 3.5 deciliters into centiliters. 

Solution : 

Here, we convert bigger unit into smaller unit. So we have to multiply.

3.5 deciliters  =  3.5 x 10 centiliters

3.5 deciliters  =  35 centiliters

Example 7 :

David travels 60 miles in two hours. How many yards of distance will he cover in one minute ? 

Solution : 

Distance covered in 2 hours  =  60 miles 

Distance covered in 1 hour  =  30 miles

We know that 1 hour  =  60 minutes and 1 mile  =  1760 yards

1 hour ---> 30 miles ===> 60 minutes -----> 30 x 1760 yards

60 minutes -----> 52800 yards

So, distance covered in 60 minutes  =  52800 yards

Distance covered in one minute  =  52800 / 60 yards 

=  880 yards

Example 8 : 

Mark jogged 15840 feet in 45 minutes. Find the speed of Mark in feet per minute. 

Solution : 

Speed  =  Distance / Time

Speed  =  15840 / 45

Speed  =  352 feet per minute

Example 9 : 

Use a fraction to find the length in meters of a tile that is 9 centimeters long. 

Solution : 

Here, we convert smaller unit (centimeters)  into bigger unit (meters). So we have to divide.

Since we divide, we have to use the fraction 1/100.

Because, 1 meter  =  100 centimeters

9 centimeters  =  9 x 1/100 meters

9 centimeters  =  9/100 meters

Example 10 : 

Kevin has a pole that is 24 meters tall. If Kevin sets the pole on a 300 centimeters stand, how far from the floor will the top of the pole be (in meters) ?

Solution : 

Height of the pole  =  24 meters

Height of the stand  = 300 centimeters  =  300/100 =  3 m

Distance from the floor to the top of the pole is 

=  Height of the stand + Height of the pole

=  30 + 3 

=  33 meters

Example 11 : 

While lifting weights, John adds 11.35 kilograms to his bar. About how many pounds does he add to his bar?

Solution :

Find the conversion factor.

1 pound ≈ 0.454 kilogram

Write the conversion factor as a ratio:

= 1 pound/0.454 kilogram

11.35 kilograms = 1 pound / 0.454 kilogram

= 25 pounds

John adds about 25 pounds in his bar.

Example 12 : 

Bob’s driveway is 45 feet long by 18 feet wide. He plans to pave the entire driveway. The asphalt paving costs $24 per square meter. What will be the total cost of the paving?

Solution :

Area  of drive way = length x width

= 45 x 18

= 810 square feet

Cost of paving = $24 per square feet

Total cost = 810 x 24

= $19440

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.