CONSTRUCTION OF TRIANGLE WHEN THREE SIDES ARE GIVEN

The way of constructing a triangle is depending on the information given.

Here we are going to see, how to construct a triangle when the lengths of all the three sides are given.

Before we start constructing the triangle, we have to check the following important property of triangle is met by the lengths of all the three sides.

"The sum of any two sides of a triangle is always greater than the third side"

If the above mentioned property of triangle is not met by the given three sides, we will not be able to construct a triangle with those three sides. 

To construct a triangle when the lengths of all the three sides are given, we must need the following mathematical instruments. 

1. Ruler

2. Compass

The steps for the construction of a triangle when the lengths of all the three sides are given.

Example : 

Construct a triangle ABC given that AB = 4cm, BC = 6 cm and AC = 5 cm.

Given measurements :

AB  =  4cm

BC  =  6 cm

AC  =  5 cm

Step 1 :

Draw a line segment BC  =  6cm

(Here we take the longest side)

Step 2 :

With ‘B’ as centre, draw an arc of radius 4 cm above the line BC.

Step 3 :

With ‘C’ as center, draw an arc of 5 cm to intersect the previous arc at ‘A’

Step 4 :

Join AB and AC.

Now ABC is the required triangle.

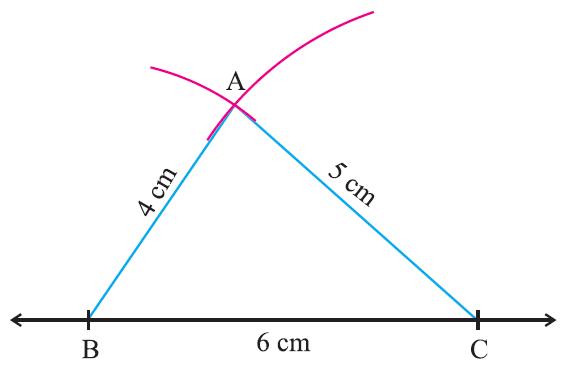
This construction clearly shows how to construct a triangle when the lengths of all the three sides are given with compass and straightedge or ruler. 

A student attempted to draw a triangle with given measurements PQ = 2 cm, QR = 6 cm, PR = 3 cm. First he drew QR = 6cm. Then he drew an arc of 2cm with Q as centre and he drew another arc of radius 3 cm with R as centre. They could not intersect each to get P.

What is the reason ?

Given measurements :

PQ  =  2 cm

QR  =  6 cm

PR  =  3 cm

Step 1 :

Draw a line segment QR  =  6cm.

(Here we take the longest side)

Step 2 :

With ‘R’ as centre, draw an arc of radius 3 cm above the line QR.

Step 3 :

With ‘Q’ as center, draw an arc of c cm above the line QR

Step 4 :

Now, the arc said in step 2 and arc said in step 3 must intersect.

Let us apply the above steps and see whether the two arcs intersect. 

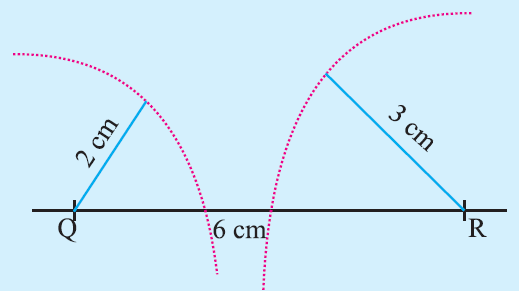
In the above figure, the two arcs said in step 2 and step 3 do not intersect. 

Since the two arcs do not intersect, we can not draw a triangle with the given the three sides. 

Reason : 

According to the property of triangles, we have that he sum of any two sides of a triangle is always greater than the third side.

But here, the sum of the two sides 2 and 3 is less than the third side 6. 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.