CONSTANT SPEED
Constant speed is also called as uniform rate which involves something travelling at fixed and steady pace or else moving at some average speed.
For example, A car travels 3 hours. It travels 30 miles in the first hour, 45 miles in the second hour and 75 miles in the third hour.
Speed in the first hour = 30 miles / hour
Speed in the second hour = 45 miles / hour
Speed in the third hour = 75 miles / hour
We have three different speeds in the three hour journey.
If we want to find the constant speed for the whole journey of three hours, we have to find the ratio between the total distance covered and total time taken.
That is, constant speed = (30 + 45 + 75) / 3
= 150 / 3
= 50 miles / hour
Based on the above example, the formula is to find the constant speed is given below.
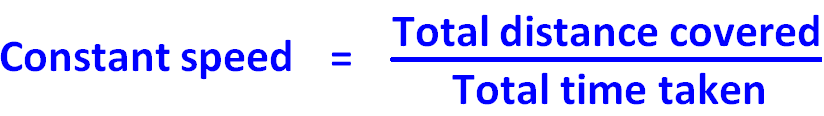
If a person travels from A to B at some speed, say "x" miles per hour. He comes back from B to A at different speed, say "y" miles per hour. Both the ways, he covers the same distance, but at different speeds.
Then, the formula is to find the constant speed for the whole journey is given below.
Constant Speed - Examples
Example 1 :
David drove for 3 hours at a rate of 50 miles per hour, for 2 hours at 60 miles per hour and for 4 hours at a rate of 70 miles per hour. What was his constant-speed for the whole journey ?
Solution :
Step 1 :
Formula for constant-speed = Total distance / Total time taken.
And also, for for distance = Rate x Time
Step 2 :
Distance covered in the first 3 hours :
= 50 x 3
= 150 miles
Distance covered in the next 2 hours :
= 60 x 2
= 120 miles
Distance covered in the last 4 hours :
= 70 x 5
= 350 miles
Step 3 :
Then, total distance is
= 150 + 120 + 350
= 620 miles
Total time is
= 3 + 2 + 5
= 10 hours
Step 4 :
So, constant speed is
= 620 / 10
= 62 miles per hour
Therefore, the constant speed for the whole journey is 62 miles per hour.
Example 2 :
A person travels from Newyork to Washington at the rate of 45 miles per hour and comes backs to the Newyork at the rate of 55 miles per hour. What is the constant speed for the whole journey ?
Answer :
Step 1 :
Here, both the ways, he covers the same distance.
Then, the formula to find average speed is
= 2xy / (x+y)
Step 2 :
x ----> Rate at which he travels from Newyork to Washington
x = 45
y ----> Rate at which he travels from Newyork to Washington
y = 55
Step 3 :
So, the average speed is
= (2 ⋅ 45 ⋅ 55) / (45 + 55)
= 4950 / 100
= 49.5
So, the constant speed for the whole journey is 45 miles per hour.
Example 3 :
A man takes 10 hours to go to a place and come back by walking both the ways. He could have gained 2 hours by riding both the ways. The distance covered in the whole journey is 18 miles. Find the constant speed for the whole journey if he goes by walking and comes back by riding.
Solution :
Step 1 :
Given : A man takes 10 hours to go to a place and come back by walking both the ways.
That is,
Walking + Walking = 10 hours
2 ⋅ Walking = 10 hours
Walking = 5 hours
Given : He could have gained 2 hours by riding both the ways.
That is,
Riding + Riding = 8 hours
2 ⋅ Riding = 8 hours
Riding = 4 hours
Step 2 :
If he goes by walking and comes back by riding, time taken by him :
Walking + Riding = 5 + 4
Walking + Riding = 9 hours
Step 3 :
Total time taken = 9 hours
Total distance covered = 18 miles
Step 4 :
So, the average speed is
= Total distance / Total time
= 18 / 9
= 2
So, the required constant speed is 2 miles per hour.
Example 4 :
Lily takes 3 hours to travel from place A to place B at the rate of 60 miles per hour. She takes 2 hours to travel from place B to C with 50% increased speed. Find the constant-speed from place A to C.
Solution :
Step 1 :
Speed ( from A to B ) = 60 miles/hour
Speed ( from B to C ) = 90 miles/hour (50% increased)
Step 2 :
Formula to find distance is
= Rate ⋅ Time
Distance from A to B is
= 60 ⋅ 3
= 180 miles
Distance from B to C
= 90 ⋅ 2
= 180 miles
Total distance traveled from A to B is
= 180 + 180
= 360 miles
Total time taken from A to B is
= 3 + 2
= 5 hours
Step 3 :
Formula to find average speed is
= Total distance / Total time
= 360 / 5
= 72
So, the constant speed from place A to B is 72 miles/hour.
Example 5 :
A person takes 5 hours to travel from place A to place B at the rate of 40 miles per hour. He comes back from place B to place A with 25% increased speed. Find the constant speed for the whole journey.
Solution :
Step 1 :
Speed ( from A to B ) = 40 miles/hour
Speed ( from B to A ) = 50 miles/hour (25% increased)
Step 2 :
The distance traveled in both the ways (A to B and B to A) is same.
So, the formula to find average distance is
= 2xy / (x + y)
Step 3 :
x ----> Speed from place A to B
x = 40
y ----> Speed from place B to A
y = 50
Step 4 :
Average speed = (2 ⋅ 40 ⋅ 50) / (40 + 50)
Average speed = 44.44
So, the constant speed for the whole journey is about 44.44 miles/hour.
Example 6 :
Distance from A to B = 200 miles,
Distance from B to C = 300 miles,
Distance from C to D = 540 miles
The speed from B to C is 50% more than A to B. The speed from C to D is 50% more than B to C. If the speed from A to B is 40 miles per hour, find the constant-speed from A to D.
Solution :
Step 1 :
Speed ( from A to B ) = 40 miles/hour
Speed ( from B to C ) = 60 miles/hour (50% more)
Speed ( from C to D ) = 90 miles/hour (50% more)
Step 2 :
Formula to find time is
= Distance / Time
Time (A to B) = 200 / 40 = 5 hours
Time (B to C) = 300 / 60 = 5 hours
Time (C to D) = 540 / 90 = 6 hours
Total time taken from A to D is
= 5 + 5 + 6
= 16 hours
Total distance from A to D is
= 200 + 300 + 540
= 1040 miles
Step 3 :
Formula to find average speed is
= Total distance / Total time
= 1040 / 16
= 65
So, the average speed from A to D is 65 miles per hour.
Apart from the stuff given above, if you need any other stuff, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Using Translation Vectors to Transform Figures Worksheet
Aug 02, 21 07:10 AM
Using Translation Vectors to Transform Figures Worksheet
-
Find Translation of a Point Along the Given Vector
Aug 02, 21 05:03 AM
Find Translation of a Point Along the Given Vector
-
Translation of the Image Under the Point Practice Problems
Aug 02, 21 04:03 AM
Translation of the Image Under the Point Practice Problems
