CONGRUENT TRIANGLES

If two triangles are congruent, then they have to satisfy the following conditions.  

1. They must have exactly the same three sides.

2. They must have exactly the same three angles.

3. If there is a turn or flip, the equal sides and angles may not be in the same position. But they must be there.

If two triangles meet the first and second conditions, then they are said to be congruent triangles. 

Triangle Congruence Postulates and Theorems

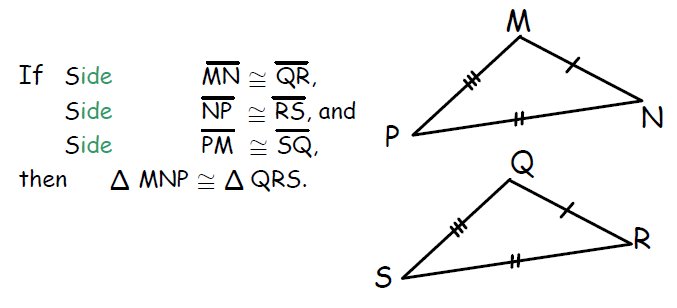
1. Side-Side-Side (SSS) Congruence Postulate

If three sides of one triangle is congruent to three sides of another triangle, then the two triangles are congruent.

2. Side-Angle-Side (SAS) Congruence Postulate

If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.

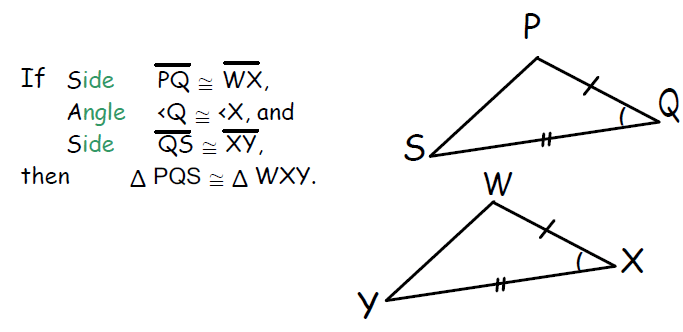
3. Angle-Side-Angle (ASA) Congruence Postulate

If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.

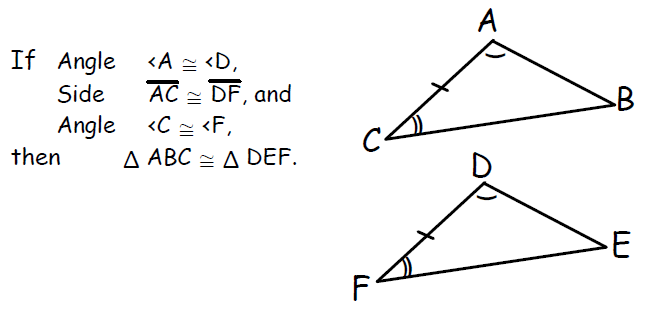
4. Angle-Angle-Side (AAS) Congruence Postulate

If two angles and non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent.

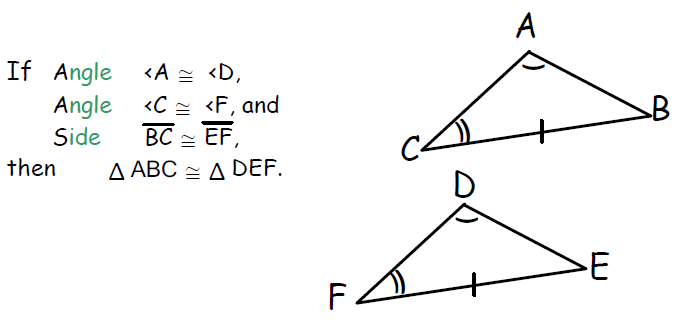
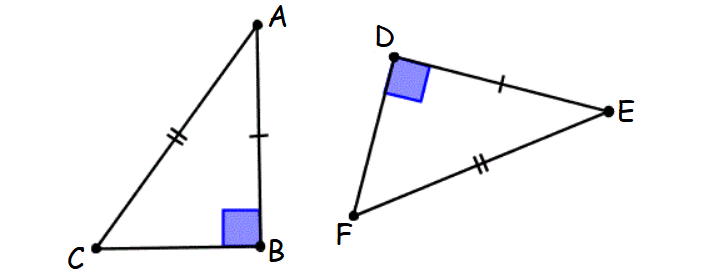
5. Hypotenuse-Leg (HL) Theorem

If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

This principle is known as Hypotenuse-Leg theorem. 

6. Leg-Acute (LA) Angle Theorem

If a leg and an acute angle of one right triangle are congruent to the corresponding parts of another right triangle, then the two right triangles are congruent.

This principle is known as Leg-Acute Angle theorem.

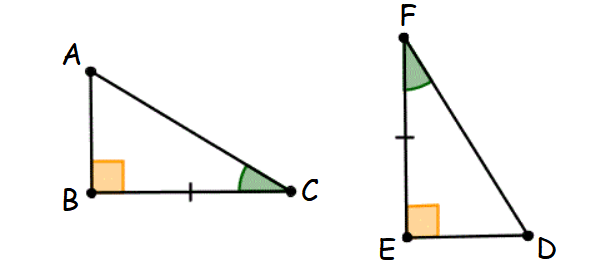
7. Hypotenuse-Acute (HA) Angle Theorem

If the hypotenuse and an acute angle of a right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the two triangles are congruent.

This principle is known as Hypotenuse-Acute Angle theorem. 

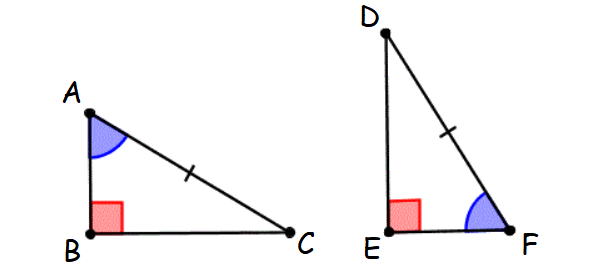
8. Leg-Leg (LL) Theorem

If the legs of one right triangle are congruent to the legs of another right triangle, then the two right triangles are congruent.

This principle is known as Leg-Leg theorem. 

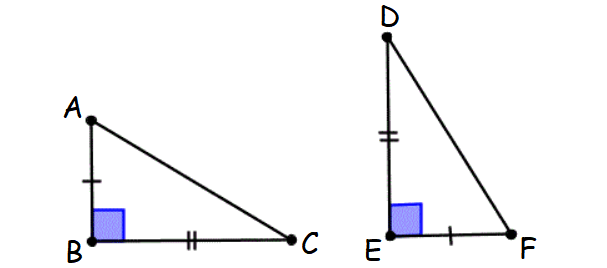
Caution

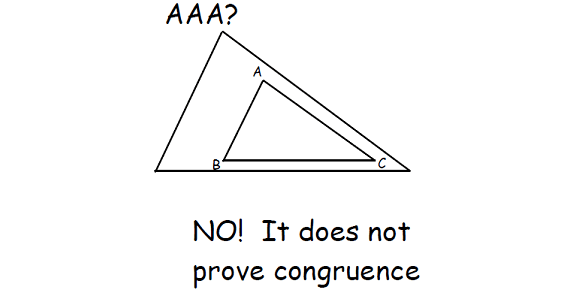
SSA and AAA can not be used to test congruent triangles.

Let us see, how SSA does not prove congruence. Please look at the picture given below. 

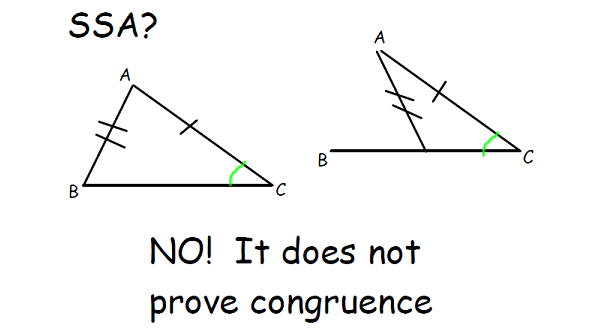
The above picture clearly illustrates that SSA does not prove congruence. When we look at the picture above, we do not need words to understand why SSA does not prove the congruence.

Because the picture itself clearly speaks the fact. We hope that the students can understand everything from the picture.

Now, let us see, how AAA does not prove congruence. Please look at the picture given below.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.