POINT OF CONCURRENCY
We know that two non parallel lines intersect at a point. If a third line is drawn passing through the same point, these straight lines are called concurrent-lines.
In the figure shown below, the straight lines AB, CD and EF are passing through one point P.
So, the point P is the point of concurrency.
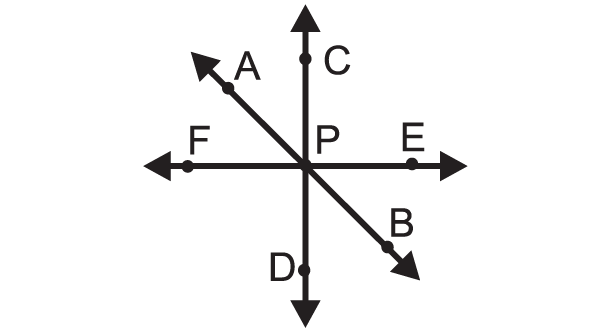
Example 1 :
In the figure shown below, find the concurrent lines and point of concurrency.
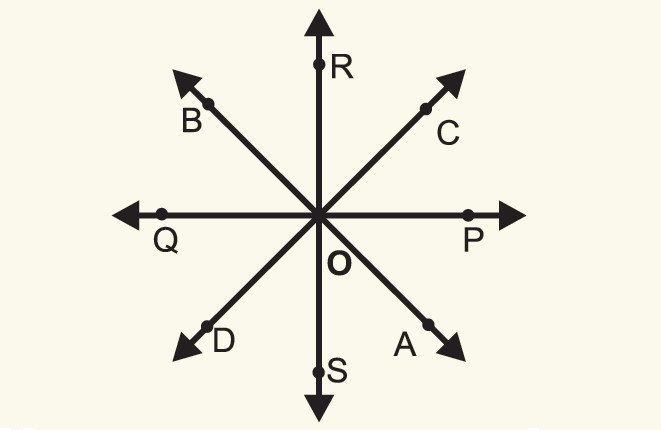
Solution :
In the diagram above, since the straight lines AB, CD, PQ and RS are all meeting at the same point O, they are concurrent line.
The point of concurrency is O.
Example 2 :
Prove that the following lines are concurrent and find the point of concurrency.
3x - 4y + 5 = 0
7x - 8y + 5 = 0
4x + 5y = 45
Solution :
3x - 4y + 5 = 0 ----A
7x - 8y + 5 = 0 ----B
4x + 5y - 45 = 0 ----C
Solve A and B :
B - 2A ----> x - 5 = 0
x = 5
Substitute x = 5 in (1).
3(5) - 4y + 5 = 0
15 - 4y + 5 = 0
20 - 4y = 0
-4y = -20
y = 5
The point of intersection of A and B is (5, 5).
Now, check whether the line C satisfies the point (5, 5).
Substitute x = 5 and y = 5 in C,
4(5) + 5(5) = 45 (true ?)
20 + 25 = 45 (true ?)
45 = 45 (yes, it is true)
Point of intersection of lines A and B satisfies the third line.
Therefore, all the three lines A, B and C are intersecting at the same point (5, 5) and they are concurrent.
The point of concurrency is (5, 5).
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Printable Math Worksheets
Apr 20, 24 12:02 AM
Printable Math Worksheets - Worksheets in Pdf formats from grade 1 to 10 -
Printable Math Worksheets for Grade 2
Apr 19, 24 11:58 PM
Printable Math Worksheets for Grade 2 -
Sequences and Series
Apr 19, 24 11:45 PM
Sequences and Series - Concept - Examples