COMPLEMENTARY ANGLES

Two angles are complementary, if they add up to 90⁰.

Example :

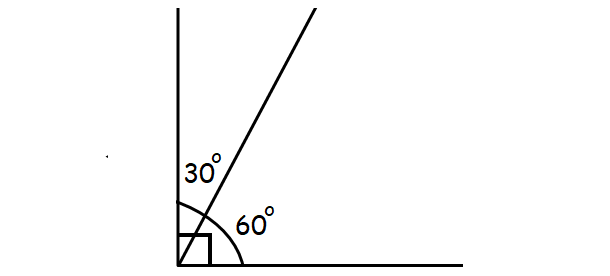
30° and 60° are complementary angles.

Because,

30° + 60° = 90°

Clearly, 30° is the complement of 60° and 60° is the complement of 30°.

Problem 1 :

The measure of an angle is 41°. What is the measure of a complementary angle?

Solution :

Let x be the measure of the required complementary angle.

Because x and 41° are complementary angles,

x + 41° = 90°

Subtract 41° from each side.

x = 49°

So, the measure of the complementary angle is 49°.

Problem 2 :

The measure of an angle is 62°. What is the measure of a complementary angle?

Solution :

Let x be the measure of the required complementary angle.

Because x and 62° are complementary angles,

x + 62° = 90°

Subtract 62° from each side.

x = 28°

So, the measure of the complementary angle is 28°.

Problem 3 :

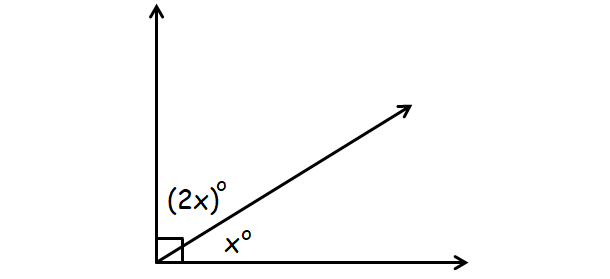
Find the value of  x :

Solution :

From the picture above, it is clear that the angles x and 2x are complementary.

x + 2x = 90°

3x = 90

Divide each side by 3.

x = 30

So, the value of x is 30.

Problem 4 :

Find the value of  x :

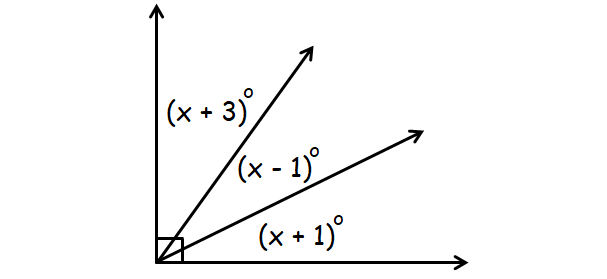
Solution :

In the picture above, the angles

(x + 1)°, (x - 1)° and (x + 3)°

are complementary.

(x + 1)° + (x - 1)° + (x + 3)° = 90°

(x + 1) + (x - 1) + (x + 3) = 90

x + 1 + x - 1 + x + 3 = 90

3x + 3 = 90

Subtract 3 from each side.

3x  =  87

Divide each side by 3.

x  =  29

So, the value of x is 29.

Problem 5 :

Two angles are complementary. If one of the angles is double the other angle, find the two angles.

Solution :

Let x be one of the angles.

Then the other angle is 2x.

Because x and 2x are complementary angles, we have

x + 2x = 90°

3x = 90

Divide each side by 3.

x = 30

And,

2x = 2(30) = 60

So, the two angles are 30° and 60°.

Problem 6 :

Two angles are complementary. If one angle is two times the sum of other angle and 3, find the two angles.

Solution :

Let x and y be the two angles which are complementary.

x + y = 90° ----(1)

Given : One angle is two times the sum of other angle and 3.

x = 2(y + 3)

x = 2y + 6 ----(2)

Now, substitute (2y + 6) for x in (1).

2y + 6 + y = 90

3y + 6 = 90

Subtract 6 from each side.

3y = 84

Divide each side by 3.

y = 28

Substitute 28 for y in (2).

x = 2(28) + 6

x = 56 + 6

x = 62

So, the two angles are 62° and 28°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.