CENTROID OF A TRIANGLE

The centroid of a triangle is the point of concurrency of the medians.

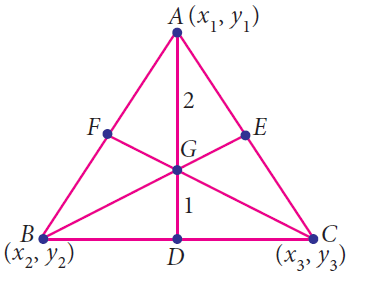
In the above triangle , AD, BE and CF are called medians. All the three medians AD, BE and CF are intersecting at G. So  G is called centroid of the triangle

If the coordinates of A, B and C are (x_1, y₁), (x_2, ,y₂) and (x₃, y₃), then the formula to determine the centroid of the triangle is given by

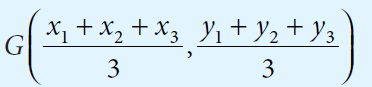
Examples

Example 1 :

Find the centroid of a triangle whose vertices are the points (8, 4), (1, 3) and (3, -1).

Solution :

Formula to find centroid of a triangle is

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

x₁  =  8, x₂  =  1 and x₃  =  3

y₁  =  4, y₂  =  3 and y₃  =  -1

=  [(8 + 2 + 3)/3, (4 + 3 - 1)/3]

=  (12/3, 6/3)

=  (4, 2)

So, the centroid of the given triangle is (4, 2). 

Example 2 :

Find the centroid of a triangle whose vertices are the points (6, -1), (8, 3) and (10, -5).

Solution :

Formula to find centroid of a triangle is

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

x₁  =  6, x₂  =  8 and x₃  =  10

y₁  =  -1, y₂  =  3 and y₃  =  -5

Then, 

=  [(6 + 8 + 10)/3, (-1 + 3 - 5)/3]

=  (24/3, -3/3)

=  (8, -1)

So, the centroid of the given triangle is (8, -1). 

Example 3 :

If a triangle has its centroid at (4, 3) and two of its vertices are (2, -1) and (7, 8), find the third vertex.

Solution :

Let (a, b) be the third vertex.

Centroid of the triangle  =  (4, 3)

[(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]  =  (4, 3)

x₁  =  2, x₂  =  7 and x₃  =  a

y₁  =  -1, y₂  =  8 and y₃  =  b

Then,

[(2 + 7 + a)/3, (-1 + 8 + b)/3]  =  (4, 3)

[(9 + a)/3, (7 + b)/3]  =  (4, 3)

Equate the coordinates of x and y. 

So, the third vertex is (3, 2).

Example 4 :

If the centroid of a triangle is (-2, 1) and two of its vertices are (1, -6) and (-5, 2), then find the third vertex.

Solution :

Let (a, b) be the third vertex.

Centroid of the triangle  =  (-2, 1)

[(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]  =  (-2, 1)

x₁  =  1, x₂  =  -5 and x₃  =  a

y₁  =  -6, y₂  =  2 and y₃  =  b

Then,

[(1 - 5 + a)/3, (-6 + 2 + b)/3]  =  (-2, 1)

[(-4 + a)/3, (-4 + b)/3]  =  (-2, 1)

Equate the coordinates of x and y. 

So, the third vertex is (-2, 7).

Example 5 :

Master gave a triangular plate with vertices (5, 8), (2, 4) and (8, 3) and a stick to a student. He wants to balance the plate on the stick. Can you help the boy to locate that point which can balance the plate ?

Solution :

The point which can balance the triangular plate is the centroid of the triangle. 

Formula to find centroid of a triangle is

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

x₁  =  5, x₂  =  2 and x₃  =  8

y₁  =  8, y₂  =  4 and y₃  =  3

=  [(5 + 2 + 8)/3, (8 + 4 + 3)/3]

=  (15/3, 15/3)

=  (5, 5)

So, the point which can balance the triangular plate is (5, 5). 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.