AREA OF QUADRILATERAL
A plane figure bounded by four sides is known as a quadrilateral. The straight line joining the opposite corners is called its diagonal. The diagonal divides the quadrilateral in to two triangles.
Area of Quadrilateral General Formula
Let us derive the area of quadrilateral general formula. Consider the quadrilateral ABCD shown below :
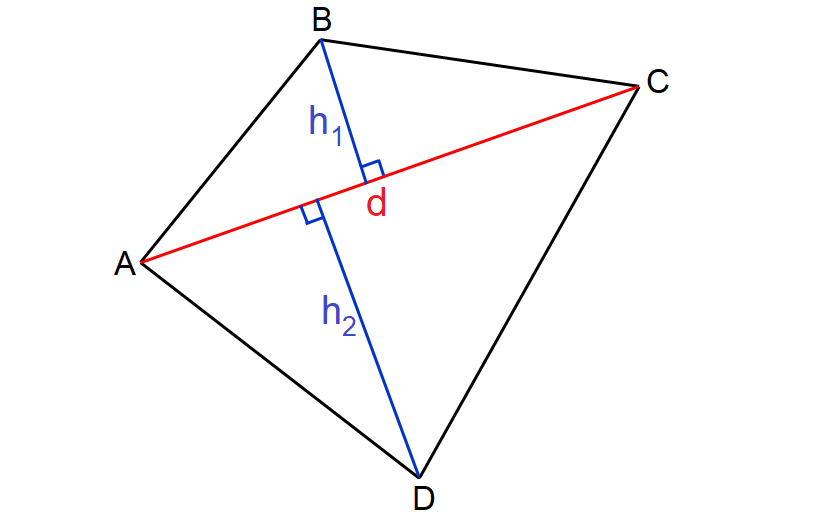
We can observe the quadrilateral above as a combination of two triangles, considering the diagonal AC (or d) as common base. h1 and h2 are the heights of the two triangles.
Area of quadrilateral ABCD above can be calculated by adding the areas of two two triangles ABC and ADC.
The area of quadrilateral ABCD is
= Area of Δ ABC + Area of Δ ADC
= 1/2 ⋅ d ⋅ h1 + 1/2 ⋅ d ⋅ h2
= = 1/2 ⋅ d ⋅ (h1 + h2)
Area of quadrilateral general formula :
= 1/2
x
length of the diagonal
x
sum of the lengths of perpendiculars drawn to the diagonal
Here is the list of the formulas to find the area of quadrilaterals such as square, rectangle, parallelogram, trapezoid, kite and rhombus.
Square
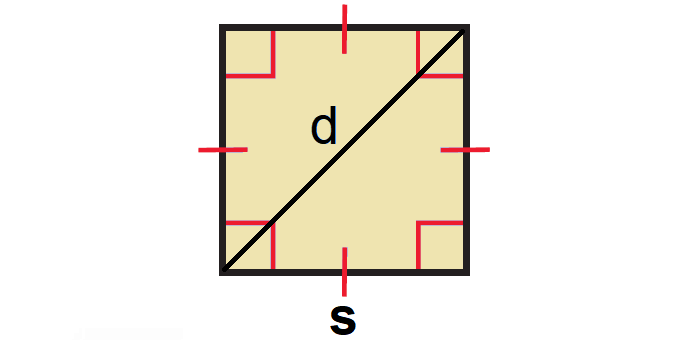
The area of a square is the product of the lengths of its two sides or square of the length of its diagonal.
Area = s ⋅ s = s2
Area = 1/2 ⋅ d2
Rectangle
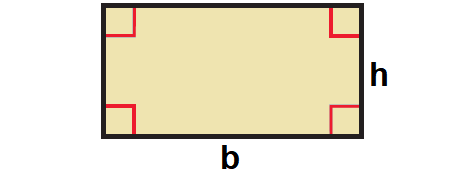
The area of a rectangle is the product of its base and height.
Area = b ⋅ h
Parallelogram
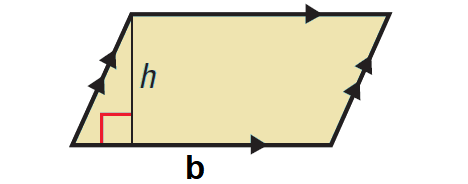
The area of a parallelogram is the product of a base and its corresponding height.
Area = b ⋅ h
Trapezoid (Trapezium)
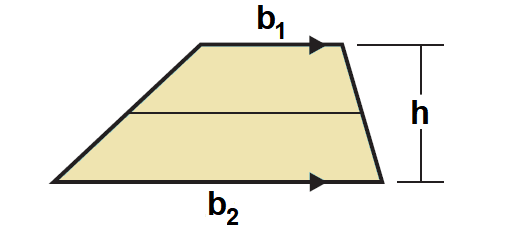
The area of a trapezoid is one half the product of the height and sum of the bases.
Area = 1/2 ⋅ h ⋅ (b1 + b2)
Kite
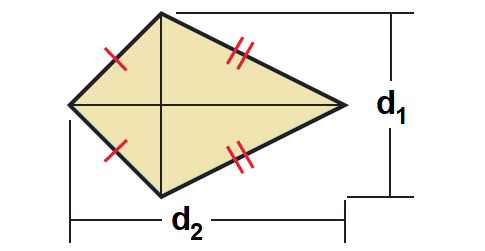
The area of a kite is one half the product of the lengths of its diagonals.
Area = 1/2 ⋅ d1 ⋅ d2
Rhombus
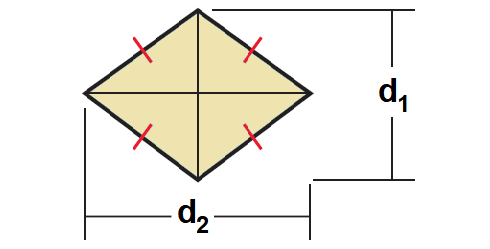
The area of a rhombus is one half the product of the lengths of its diagonals.
Area = 1/2 ⋅ d1 ⋅ d2
Apart from the stuff given above, if you need practice problems on area of quadrilaterals,
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and Venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
©All rights reserved. onlinemath4all.com
Recent Articles
-
Exponential vs Linear Growth Worksheet
May 23, 22 01:59 AM
Exponential vs Linear Growth Worksheet
-
Linear vs Exponential Growth
May 23, 22 01:59 AM
Linear vs Exponential Growth - Concept - Examples
-
SAT Math Questions on Exponential vs Linear Growth
May 23, 22 01:34 AM
SAT Math Questions on Exponential vs Linear Growth