AREA OF PARALLELOGRAM
A parallelogram is a quadrilateral in which opposite sides are parallel and equal in length.
In other words opposite sides of a quadrilateral are equal in length, then the quadrilateral is called a parallelogram.
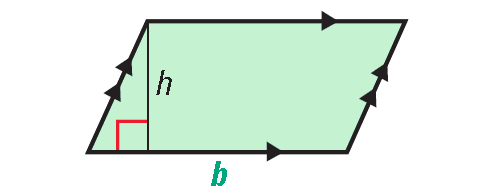
The area of a parallelogram is the product of a base and its corresponding height.
Then, the formula to find area of a parallelogram is given by
A = b ⋅ h square units
We can justify the area for parallelogram as follows.
The area of a parallelogram is the area of a rectangle with the same base and height.
Examples
Example 1 :
Find the area of the parallelogram ABCD shown below.
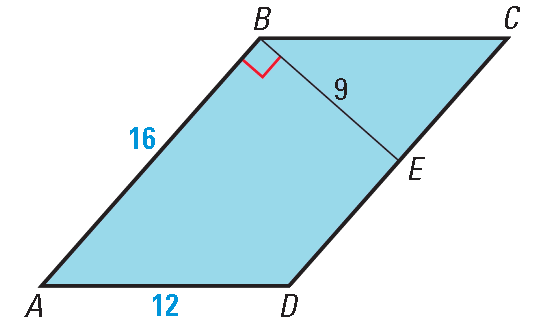
Solution :
Method 1 :
Use AB as the base.
So, b = 16 and h = 9.
Formula for area of a parallelogram is
= b ⋅ h
Substitute the given measures.
= 16 ⋅ 9
= 144 square units
Method 2 :
Use AD as the base.
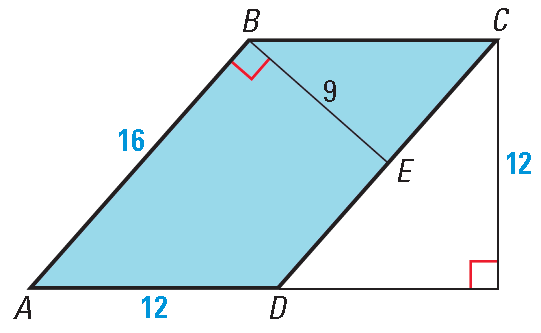
So, b = 12 and h = 12.
Formula for area of a parallelogram is
= b ⋅ h
Substitute the given measures.
= 12 ⋅ 12
= 144 square units
Example 2 :
Find the area of the parallelogram ABCD shown below.
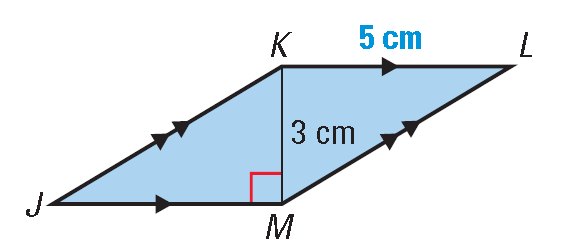
Formula for area of a parallelogram is
= b ⋅ h
Substitute b = 5 and h = 3.
= 5 ⋅ 3
= 15 square units
Example 3 :
A mirror is made of two congruent parallelograms as shown in the diagram. The parallelograms have a combined area of 9 1/3 square yards. The height of each parallelogram is 1 1/3 yards. How long is the base of each parallelogram ?
Solution :
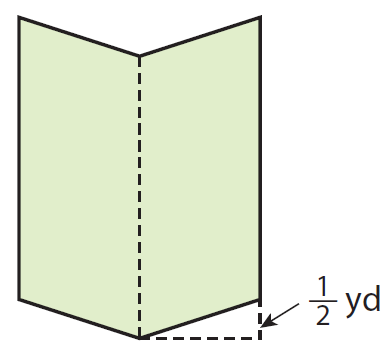
Because the given parallelograms are congruent area of two parallelogram will be equal.
Combined area of parallelograms = 9 1/3 square yards
Combined area of parallelograms = 28/3 square yards
Area of one parallelogram = (28/3) ÷ 2
Area of one parallelogram = 14/3
b ⋅ h = 14/3
b ⋅ 1 1/3 = 14/3
b ⋅ 4/3 = 14/3
Multiply each side by 3/4.
b = 14/3 ⋅ 3/4
b = 14/4
b = 7/2
b = 3 1/2
So, the base of the parallelogram is 3 1/2 yards.
Example 4 :
Find the base of a parallelogram if its area is 40 square cm and its altitude is 15 cm.
Solution :
Area of a parallelogram = 40 cm2
b ⋅ h = 40
Here, altitude (or) height (h) = 15 cm.
b ⋅ 15 = 40
Divide each side by 15.
b = 2.67
So, the base of the parallelogram is 2.67 inches.
Example 5 :
Find the area of the shape shown below.
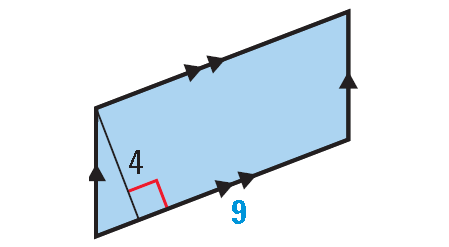
The above shape has four sides. So, it is a quadrilateral. Because the opposite sides are parallel, the above quadrilateral is a parallelogram.
Formula for area of a parallelogram is
= b ⋅ h
Substitute b = 9 and h = 4.
= 9 ⋅ 4
= 36 square units
Example 6 :
If the area of the shape shown below is 60 square inches, then find the value of x.
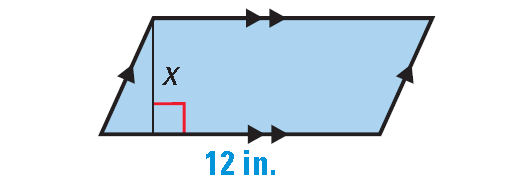
Solution :
Given : Area of the above shape is 60 square inches.
The above shape has four sides. So, it is a quadrilateral. Because the opposite sides are parallel, the above quadrilateral is a parallelogram.
Area = 60 in2
b ⋅ h = 60
Substitute b = 12 and h = x.
12 ⋅ x = 60
Divide each side by 12.
x = 5
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Adding and Subtracting Matrices Worksheet
Oct 30, 20 11:00 PM
Adding and Subtracting Matrices Worksheet
-
Greatest Common Factor
Oct 30, 20 08:10 AM
Greatest Common Factor - Concept - Methods - Examples
-
Least Common Multiple Worksheet
Oct 30, 20 04:09 AM
Least Common Multiple Worksheet
