AREA IN INTEGRATION

Steps to be Followed in Finding Area of the Curve in Integration

(i) First draw the graph of the given curve approximately. To know whether the area bounded by the region is above the x-axis, below the x-axis, left side of y-axis or right side of y-axis.

(ii) Mark the given interval in the figure.

(iii) Then write the appropriate formula

(iv) Need to integrate the function.

(v) Apply the upper and lower limits.

(vi) Put square units for the answer.

Area of the region bounded by x axis

Let y = f (x) be a continuous function defined by the closed interval [a ,b].

Then the area bounded by the curve y = f (x) is 

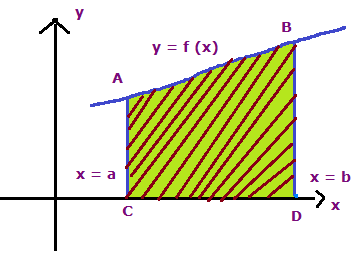
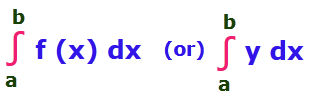
The area made by the curve above the x-axis will look like the above.

Let y  =  f(x) be a continuous function defined by the closed interval [a, b]. The area made by the curve below the x-axis will look like the below figure.

Then the area bounded by the curve y  =  -f(x) is

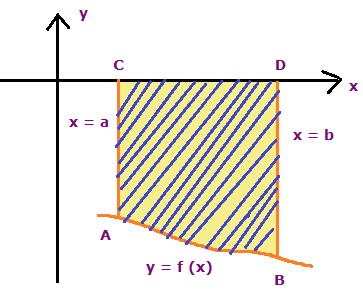
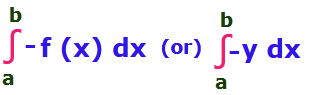
From those two figures, we can understand that

• If the required area is above the x-axis then it will be positive.
• If the required area is below the x-axis then it will be negative.

Now let us see area of curves which is right side of the y-axis and left side of the y-axis.

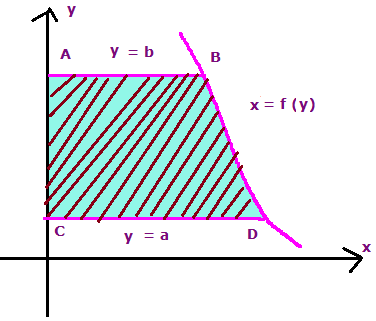
Let x = f(y) be a continuous function defined by the closed interval [a, b]. Then the area bounded by the curve x  =  f(y) is

Area of the Region Bounded by y Axis

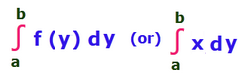
Let x  =  -f(y) be a continuous function defined by the closed interval [a, b].

Then the area bounded by the curve x = - f (y) is

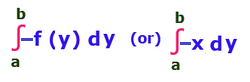
If the given curve lies left side of the y-axis with the closed interval [a, b] then area bounded by the region look like

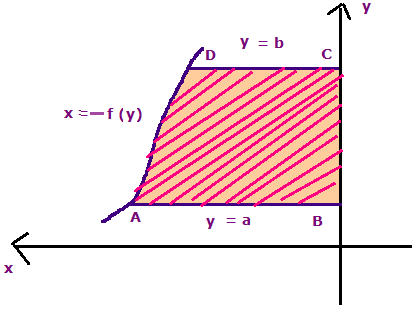
From those two figures we can understand that,

• If the required area is being right of the y-axis then it will be positive.
• If the required area is being left side of the y-axis then it will be negative.

Related pages

Area between two curves

Area bounded by two parabolas

Area enclosed by y-axis

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.