AREA BOUNDED BY TWO PARABOLAS

Example 1 :

Find the area bounded by two parabolas,

4y²  =  9x and 3x²  =  16y

Solution :

First we need to draw the rough sketch of two parabolas to find the point of intersection.

4y²  =  9x  ------ (1)

3x²  =  16y ------ (2)

4y²  =  9x

y²  =  9x/4 

y  =  3√x/2

y  =  (3/2) √x

3x²  =  16y

y  =  3x²/16

By applying the value of y in the equation y²  =  9x/4.

(3x²/16)²  =  9x/4

 9x⁴/256  =  9x/4 

 x⁴/x  =  (9 ⋅256)/(4 ⋅ 9)

x³  =  256/4

x³  =  64

x³  =   4³ 

x  =  4

By applying the value x = 4 in (1) or (2) we get the value of y

y  =  3(4)²/16

y  =  3

Therefore, the two parabolas are intersecting at the point  (0, 0) and (4, 3).

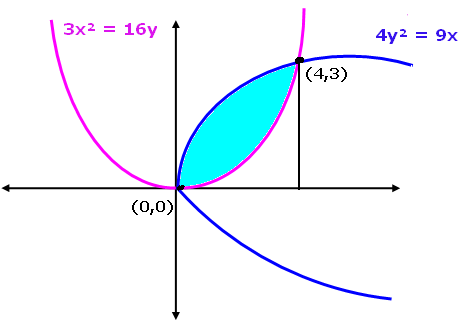
=  (3/2)[x^(3/2)/(3/2)] - (3/16) [ x^3/3 ]

=  { (3/2) [ 4^(3/2)/(3/2)]- (3/16) [4^3/3] } - 0

=  { [ (3/2) ( 4 √4 ) x (3/2) ]- (3/16) [64/3] } - 0

=  4 (2)-4

=  8-4

=  4  square units

Therefore the required area  =  4 square units.

Example 2 :

Find the area of the region bounded by the two parabolas 

y  =  x² and y²  =  x.

Solution :

y  =  x² -----(1)

y²  =  x

y  =  √x -----(2)

x²  =  √x

x⁴  =  x

x⁴ - x  =  0

x(x³-1)  =  0

x  =  0 and x  =  1

y  =  1

Point of intersection is at (0, 0) and (1, 1).

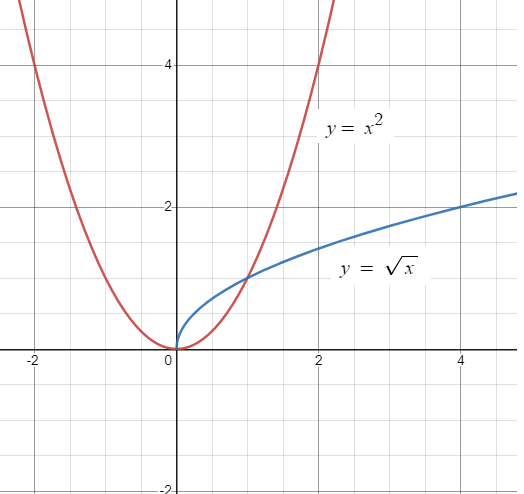
Required area  =  Integral 0 to 1 (√x - x2) dx

=  [x^3/2/(3/2) - x³/3] 0 to 1

=  0-(2/3) + 1/3

=  1/3 - 2/3

=  1/3 square units.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.