AREA AND PERIMETER WORD PROBLEMS

Problem 1 :

The length of a rectangle is 4 less than 3 times its width. If its perimeter is 32 cm, then find the area of the rectangle.

Solution :

Let x be the width of the rectangle.

Then, its length is (3x - 4).

Perimeter of the rectangle is 32 cm

2(l + w) = 32

l + w = 16

3x - 4 + x = 16

4x - 4 = 16

4x = 20

x = 5

And length of the rectangle is

= 3(5) - 4

= 15 - 4

= 11 cm

Formula for area of a rectangle :

= l ⋅ w

= 11(5)

Area = 55 cm²

Problem 2 :

Theresa wants new carpeting for her family room. Her family room is a 12 ft by 21 ft rectangle. How much carpeting does she need to buy to cover her entire family room ?

Solution :

To find the amount of carpet required, we have to know its area. Because the family room is in rectangle shape, we can use the formula for area of a rectangle to find the area of the family room.

Formula for area of a rectangle :

= l ⋅ w

Substitute 12 for l and 21 for w.

= 12(21)

= 252

So, Theresa needs to buy 252 square ft carpeting  to cover her entire family room.

Problem 3 :

Lily to wants to do fencing around a circular garden that has a radius of 70 m. If the cost of fencing is $12 per meter, find the total cost of fencing for the entire garden (Use π  =  22/7).

Solution :

Fencing is done around the circular garden. To find the total cost of fencing, we have to know the perimeter of the garden, Because the garden is in the shape of circle, we can use the formula for perimeter of a circle to find the perimeter of the garden.

Formula for perimeter of a circle :

= 2πr

Substitute 22/7 for π and 70 for r.

= 2(22/7)(70)

= 440

So, the perimeter of the garden is 440 meters.

The cost of fencing is $12 per meter.

Then, the total cost of fencing for 440 meters :

= 440(12)

= $5280

Problem 4 :

If the cost of the carpeting is $15 per square meter, find the total cost of carpeting the floor of the room whose shape is a regular pentagon shown below.

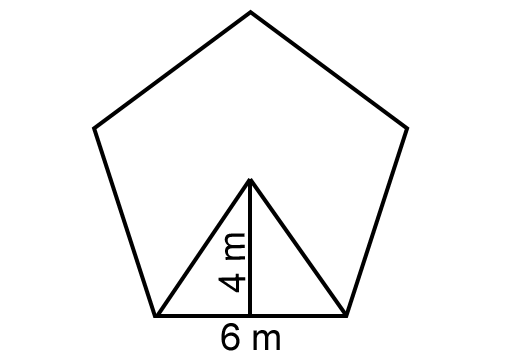
Solution :

To find the total cost of carpeting the floor of the room, we have to know its area. Because the floor of the room is in the shape of regular pentagon (regular polygon), we can use the formula for area of a regular polygon to find the area of the floor.

Formula for area of a regular polygon :

= 1/2(apothem)(perimeter of polygon) ----(1)

In the above regular pentagon, apothem is 4 m

The perimeter of a regular polygon is

= (No. of sides)(Length of each side)

Therefore, the perimeter of the regular pentagon shown above is 

= 5(6)

= 30 m

To find the area of the regular pentagon, substitute 4 for apothem and 30 for perimeter in the formula (1).

(1) ----> = 1/2(4)(30)

= 60 m²

The cost of carpeting is $15 per square meter.

Then, the total cost of carpeting for 60 square meters :

= 60(15)

= $900

Problem 5 :

The poster has a border whose width is 2 cm on each side. If the printed material has the length of 6 cm and width of 8 cm, then find the area of the border.

Solution :

Draw a sketch

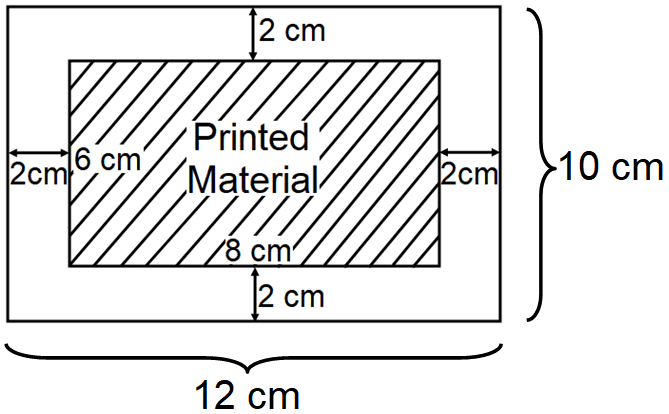
In the above diagram, to find the area of the border, we have to subtract the area of the printed material from the complete area of the poster.

Complete area of the poster :

= l ⋅ w

Substitute 10 for l and 12 for w.

= 10 ⋅ 12

= 120 cm²

Area of the printed material :

= l ⋅ w

Substitute 6 for l and 8 for w.

= 6(8)

= 48 cm²

Area of the border :

= Area of the poster - Area of the printed material

= 120 - 48

= 72 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.