ADDING FRACTIONS WITH UNLIKE DENOMINATORS
In this section, you will learn how to add fractions with different denominators.
We can use one of the following methods to add fractions with unlike denominators.
1. Cross-Multiplication method
2. LCM Method.
Cross-Multiplication Method
If the denominators of the fractions are co-prime or relatively prime, we have to apply this method.
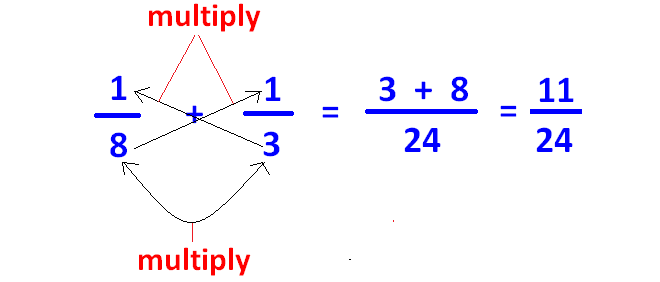
Fro example, let us consider the two fractions 1/8, 1/3.
In the above two fractions, denominators are 8 and 3.
For 8 and 3, there is no common divisor other than 1.
So 8 and 3 are co-prime.
Here we have to apply cross-multiplication method to add the two fractions 1/8 and 1/3 as shown below.
LCM Method
If the denominators of the fractions are not co-prime (there is a common divisor other than 1), we have to apply this method.
For example, let us consider the two fractions 5/12, 1/20.
In the above two fractions, denominators are 12 and 20.
For 12 and 20, if there is at least one common divisor other than 1, then 12 and 20 are not co-prime.
For 12 & 20, we have the following common divisors other than 1.
2 and 4
So 12 and 20 are not co-prime.
In the next step, we have to find the LCM (Least common multiple) of 12 and 20.
12 = 22 x 3
20 = 22 x 5
When we decompose 12 and 20 in to prime numbers, we find 2, 3 and 5 as prime factors for 12 and 20.
To get L.C.M of 12 and 20, we have to take 2, 3 and 5 with maximum powers found above.
So, the LCM of 12 and 20 is
= 22 x 3 x 5
= 4 x 3 x 5
= 60
Now, make the denominators of both the fractions as 60 using multiplication and then add them as shown below.
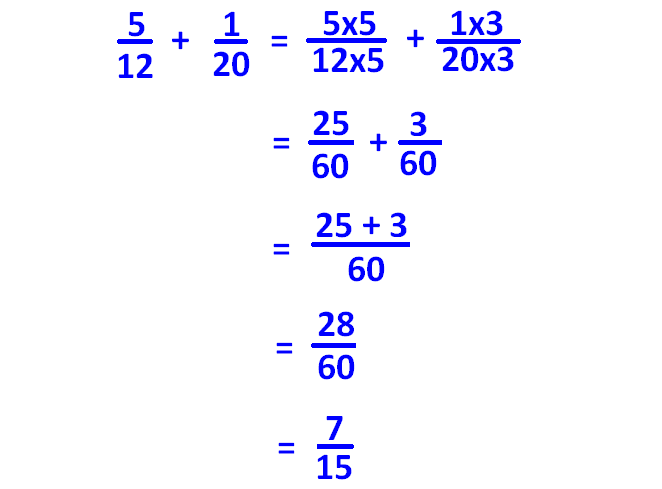
Solved Problems
Problem 1 :
Add :
1/12 + 3/18
Solution :
The given two fractions are unlike fractions. Because, they have different denominators.
For 12 and 18, we have the following common divisors other than 1.
2, 3 and 6
So 12 and 18 are not co-prime.
In the next step, we have to find the LCM (Least common multiple) of 12 and 18.
LCM of (12 and 18) = 36
Now, make the denominators of both the fractions to be 36.
To make the denominator to be 36, we have to multiply the numerator and denominator of the first fraction by 3 and the second one by 2.
Then, we have
1/12 + 3/18 = 3/36 + 2/36
= (3 + 2)/36
= 5/36
So, the sum of the two fractions is 5/36.
Problem 2 :
Add :
3/20 + 7/30
Solution :
The given two fractions are unlike fractions. Because, they have different denominators.
For 20 and 30, we have the following common divisors other than 1.
2, 5 and 10
So 20 and 30 are not co-prime.
In the next step, we have to find the L.C.M (Least common multiple) of 20 and 30.
LCM of (20 and 30) = 60
Now we have to make the denominators of both the fractions to be 60.
To make the denominator to be 60, we have to multiply the numerator and denominator of the first fraction by 3 and and for the second fraction by 2.
Then, we have
3/20 + 7/30 = 9/60 + 14/60
= (9 + 14)/60
= 23/60
So, the sum of the two fractions is 23/60.
Problem 3 :
Add :
3/7 + 2/9
Solution :
The given two fractions are unlike fractions. Because, they have different denominators.
For 7 and 9, there is no common divisor other than 1.
So 7 and 9 are co-prime
Here, we have to apply cross multiplication method to add the two fractions.
To add the two fractions, we have to do the following three steps.
Step 1 :
Multiply the numerator of the first fraction by denominator of the second fraction.
Step 2 :
Multiply the numerator of the second fraction by denominator of the first fraction.
Step 3 :
Multiply the denominators of the two fractions.
When we do the above three steps, we will have
3/7 + 2/9 = (27 + 14)/63
= 41/63
So, the sum of the two fractions is 41/63.
Problem 4 :
Add :
1/2 + 7/3 + 4/5
Solution :
The denominators of all the fractions are not same.
In this problem, we have more than two fractions.
If we have more than two fractions, we can use only L.C.M method.
In the next step, we have to find the L.C.M (Least common multiple) of 2, 3 and 5.
LCM of (2, 3 and 5) = 30
Now we have to make the denominators of all the three fractions to be 30.
To make the denominator to be 30, we have to multiply the numerator and denominator of the first fraction by 15, for the second fraction by 10 and for the third fraction by 6.
Then, we have
1/2 + 7/3 + 4/5 = 15/30 + 70/30 + 24/30
= (15 + 70 + 24)/30
= 109/30
So, the sum of the two fractions is 109/30.
Problem 5 :
Add :
1/9 + 7/10 + 4/9
Solution :
The denominators of all the fractions are not same.
In this problem, we have more than two fractions.
If we have more than two fractions, we can use only LCM method.
In the next step, we have to find the LCM (Least common multiple) of 9, 10 and 9.
LCM of (9, 10 and 9) = 90
Now we have to make the denominators of all the three fractions to be 90.
To make the denominator to be 90, we have to multiply the numerator and denominator of the first fraction by 10, for the second fraction by 9 and for the third fraction by 10.
Then, we have
1/9 + 7/10 + 4/9 = 10/90 + 63/90 + 40/90
= (10 + 63 + 40)/90
= 113/90
So, the sum of the two fractions is 113/90.
Worksheets
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number -
Complex Plane
Apr 14, 24 07:56 AM
Complex Plane