ADDING FRACTIONS WITH LIKE DENOMINATORS
In this section, you will learn, how to add fractions with the same denominator.
Consider the figures shown below.
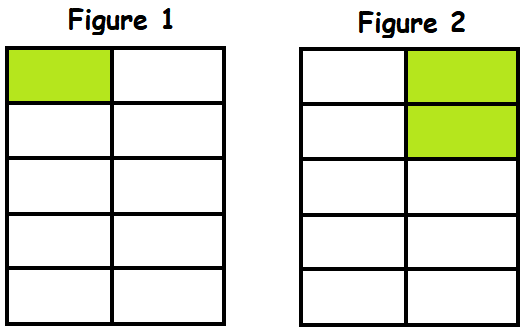
In figure 1, the shaded portion can be represented by the fraction 1/10.
In figure 2, the shaded portion can be represented by the fraction 2/10.
Combine the shaded portions in both figure 1 and figure 2 as shown below.
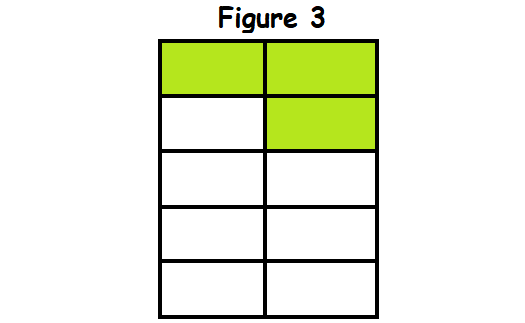
Now, the shaded portion in the above figure 3 can be represented by the fraction 3/10.
That is,
1/10 + 2/10 = 3/10
Using the above example, we can define the following steps to add two or more fractions with the same denominator.
The following steps will be useful to add fractions with the same denominators.
Step 1 :
When two or more more fractions with the same denominator are added, take the denominator once.
Step 2 :
Now, add the numerators and simplify, if required.
Example 1 :
Find the value of :
1/5 + 2/5
Solution :
1/5 + 2/5
The given two fractions have the same denominator. That is 5.
So, take the denominator once and add the numerators.
= (1 + 2)/5
= 3/5
Therefore,
1/5 + 2/5 = 3/5
Example 2 :
Add 5/14 and 2/14.
Solution :
5/14 + 2/14
The given two fractions have the same denominator. That is 14.
So, take the denominator once and add the numerators.
= (5 + 2)/14
= 7/14
Simplify.
= 1/2
Therefore,
5/14 + 2/14 = 1/2
Example 3 :
Find the value of :
1/5 + 2/5 + 2/5
Solution :
1/5 + 2/5 + 2/5
The given fractions have the same denominator. That is 5.
So, take the denominator once and add the numerators.
= (1 + 2 + 2)/5
= 5/5
Simplify.
= 1
Therefore,
1/5 + 2/5 + 2/5 = 1
Example 4 :
Find the value of :
2/13 + 7/13 + 12/13 + 5/13
Solution :
2/13 + 7/13 + 12/13 + 5/13
The given fractions have the same denominator. That is 13.
So, take the denominator once and add the numerators.
= (2 + 7 + 12 + 5)/13
= 26/13
Simplify.
= 2
Therefore,
2/13 + 7/13 + 12/13 + 5/13 = 2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
