ABSOLUTE VALUE FUNCTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
An absolute value function is a function that contains an algebraic expression within absolute value symbols.
Recall that the absolute value of a number is its distance from 0 on the number line.
Writing an Absolute Value Function as a Piecewise Function
The absolute value parent function, written as
f(x) = |x|
can be defined as follows.
To define an absolute value function as a piecewise function, we have to check the three things given below.
1. For what value of x, the expression inside the absolute value is negative. .
2. For what value of x, the expression inside the absolute value is equal to zero.
3. For what value of x, the expression inside the absolute value is positive.
In the absolute value parent function f(x) = |x|, the expression inside the absolute value is x.
Here, we have
x is negative, when x < 0
x is equal to zero, when x = 0
x is positive, when x > 0
Therefore, f(x) = |x| can be defined as
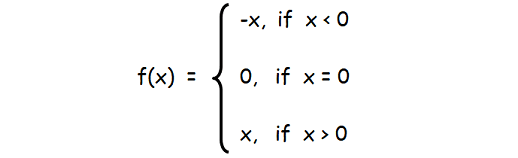
Example :
Redefine f(x) = |2x - 1| as piecewise function.
Solution :
Equate the expression inside the absolute value to zero.
2x - 1 = 0
Add 1 to each side.
2x = 1
Divide each side by 2.
x = 1/2
Here, we have
(2x - 1) is negative, when x < 1/2
(2x - 1) is equal to zero, when x = 1/2
(2x - 1) is positive, when x > 1/2
Therefore, f(x) = |2x - 1| can be defined as
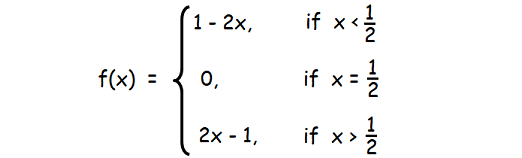
Graphing Absolute Value Functions
We have to do the following steps to graph an absolute value function.
Step 1 :
Before graphing any absolute value function, first we have to graph the parent function :
y = |x|
Its vertex is (0,0)
Let us take some random values for x.
x = - 3 -----> y = |-3| = 3 -----> (-3, 3)
x = - 2 -----> y = |-2| = 2 -----> (-3, 3)
x = - 1 -----> y = |-1| = 1 -----> (-3, 3)
x = 0 -----> y = |0| = 0 -----> (0, 0)
x = 1 -----> y = |1| = 1 -----> (1, 1)
x = 2 -----> y = |2| = 2 -----> (2, 2)
x = 3 -----> y = |3| = 3 -----> (3, 3)
If we plot these points on the graph sheet, we will get a graph as given below.
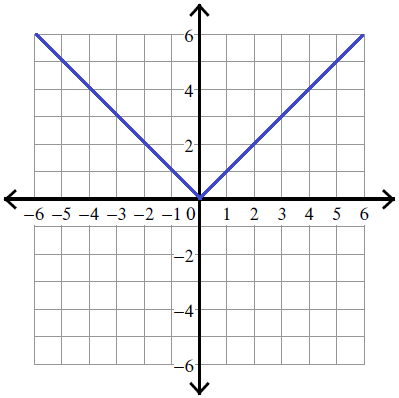
When we look at the above graph, clearly the vertex is
(0, 0)
Step 2 :
Write the given absolute value function as
y - k = |x - h|
Step 3 :
To get the vertex of the absolute value function above, equate (x - h) and (y - k) to zero,
That is,
x - h = 0 and y - k = 0
x = h and y = k
Therefore, the vertex is
(h, k)
According to the vertex, we have to shift the above graph.
Horizontal Shift :
h < 0 -----> Translate the graph h units to the left
h = 0 -----> No horizontal translation
h > 0 -----> Translate the graph h units to the right
Vertical Shift :
k < 0 -----> Translate the graph k units down
k = 0 -----> No vertical translation
k > 0 -----> Translate the graph k units up
Opens Upward / Downward :
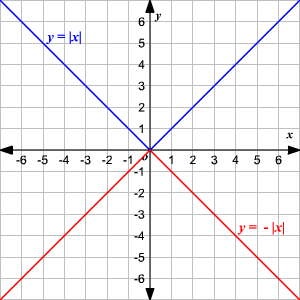
Let the given absolute value function be
y = a|x|
Then, we have
a > 0 -----> the graph opens up
a < 0 -----> the graph opens down
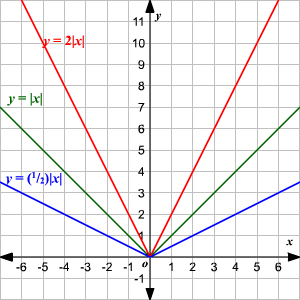
Stretch / Compression :
Let the given absolute value function be
y = a|x|
Then, we have
0 < a < 1 -----> the graph is compressed
a > 1 -----> the graph is stretched
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


