FIND THE CENTER VERTICES FOCI AND ECCENTRICITY OF THE ELLIPSE
What is ellipse ?
For two given points, the foci, an ellipse is the locus of points such that the sum of the distance to each focus is constant.
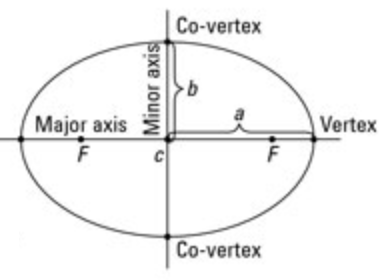
Ellipse Symmetric about x-axis :
x2/a2 + y2/b2 = 1
a > b
whose center is (0, 0).
(x-h)2/a2 + (y-k)2/b2 = 1
a > b
whose center is (h, k).
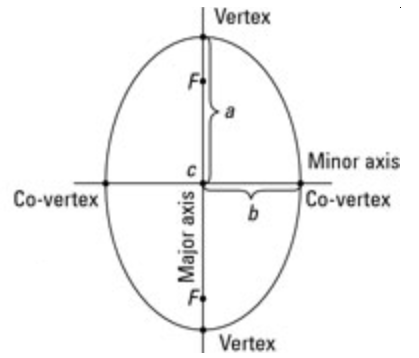
Ellipse Symmetric about y-axis :
x2/a2 + y2/b2 = 1
b > a
Center :
The point of intersection of the major axis and minor axis of the ellipse is called the center of the ellipse.
Here C(0, 0) is the center of the ellipse.
Note that the center need not be the origin of the ellipse always.
Focus :
The fixed point is called focus, denoted as
F1 (ae, 0) and F2 (-ae, 0).
Vertices :
The points of intersection of the ellipse and its major axis are called its vertices. Here the vertices of the ellipse are
A(a, 0) and A′(− a, 0).
Latus rectum :
It is a focal chord perpendicular to the major axis of the ellipse. The equations of latus rectum are x = ae, x = − ae.
Eccentricity :
e = √1 - (b2/a2)
Directrix :
The fixed line is called directrix l of the ellipse and its equation is x = a/e .
Major axis :
The line segment AA′ is called the major axis and the length of the major axis is 2a. The equation of the major axis is y = 0.
Minor axis :
The line segment BB′ is called the minor axis and the length of minor axis is 2b. Equation of the minor axis is x = 0. Note that the length of major axis is always greater than minor axis
Length of latus rectum :
The formula to find length of latus rectum is 2b2/a.
Example 1 :
Find the
(i) Center
(ii) Foci
(iii) Eccentricity
(iv) Equation of latus rectum
(v) Equation of directrix
(vi) Length of latus rectum
9x2+4y2 = 36
Solution :
Equation of ellipse :
9x2 + 4y2 = 36
(x2/4) + (y2/9) = 1
a2 = 9 and b2 = 4
a = 3 and b = 2
Since b > a, the ellipse symmetric about y-axis.
e = √1 - (4/9)
e = √( 5/9)
e = √5/3
ae = 3(√5/3)
ae = √5
a/e = 9/√5
Center : (0, 0)
Focus : F1 (√5, 0) and F2 (-√5, 0)
Eccentricity : e = √5/3
Equation of latus rectum : x = ±√5
Equation of directrix : x = ±9/√5
Length of latus rectum :
= 2(4)/3
= 8/3
Example 2 :
Find the
(i) Center
(ii) Foci
(iii) Eccentricity
(iv) Equation of latus rectum
(v) Equation of directrix
(vi) Length of latus rectum
25x2+9y2-150x-90y+225 = 0
Solution :
25x2+9y2-150x-90y+225 = 0
25x2-150x+9y2-90y+225 = 0
25(x2-6x) + 9(y2-10y) + 225 = 0
25[(x-3)2-32] + 9[(y-5)2-52] + 225 = 0
25[(x-3)2-9] + 9[(y-5)2-25] + 225 = 0
25(x-3)2-225 + 9(y-5)2-225 + 225 = 0
25(x-3)2 + 9(y-5)2 = 225
(x-3)2/9 + (y-5)2/25 = 1
Let X = x-3 and Y = y-5
x = X + 3 and y = Y + 5
The ellipse is symmetric about y-axis.
a2 = 25, b2 = 9
a = 5 and b = 3
e = √(1-9/25)
e = 4/5
ae = 4
a/e = 25/4
Length of latus rectum :
= 2(9)/5
= 18/5
|
Referred to X an Y |
Referred to x an y | |
|
Center Foci Vertices Equation of latus rectum Equation of directrix |
C(0, 0) F1(4, 0) F2(-4, 0) A(0, 5) A'(0, -5) X = 4 X = -4 X = 25/4 X = -25/4 |
C(3, -5) F1(3, 1) F2(3, 9) A(3, 10) A'(3, 0) y = 9 y = 1 y = 45/4 y = -5/4 |
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number
