PROPERTIES OF DEFINITE AND INDEFINITE INTEGRALS

Property 1 :

Integration is independent of change of variables provided the limits of integration remain the same.

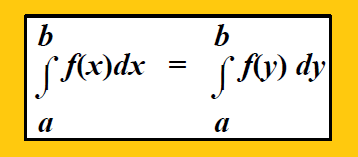
Property 2 :

If the limits of definite integral are interchanged, then the value of integral changes its sign only.

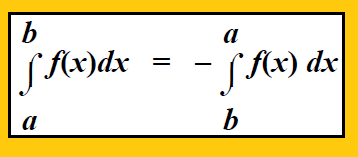
Property 3 :

Property 4 :

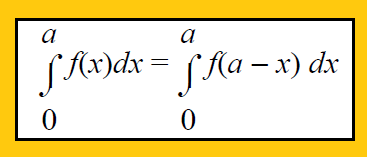
Property 5 :

If f(x) is integrable on a closed interval containing the three numbers a, b and c, then regardless of the order of a, b and c.

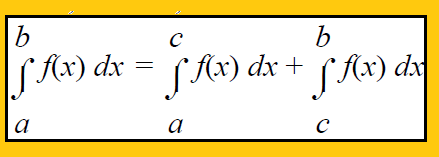
Property 6 :

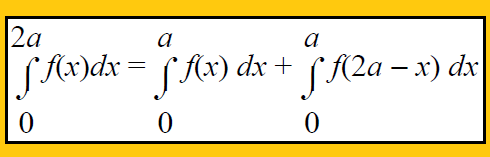
Property 7 :

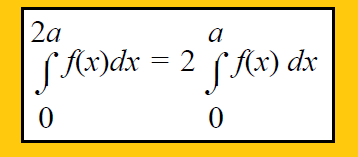
Property 8 :

To check if the function is odd or even, in the given function f(x) apply x  =  -x

• If f(-x)  =  f(x), then f(x) is even.
• If f(-x)  =  -f(x), then f(x) is odd.

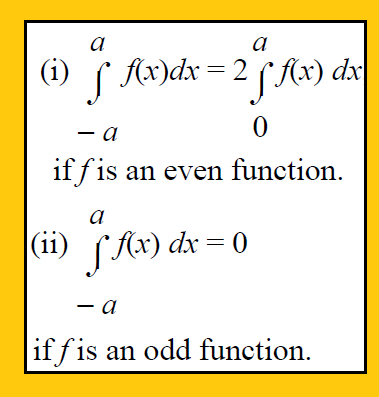
Properties of Indefinite Integrals

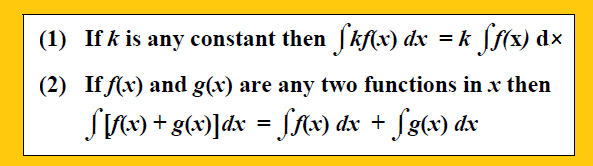
Evaluate the following problems using properties of integration.

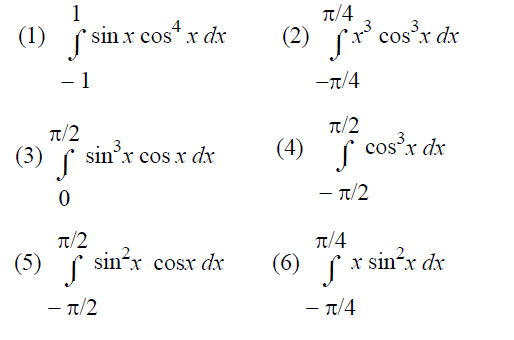
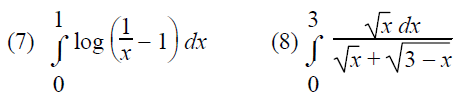
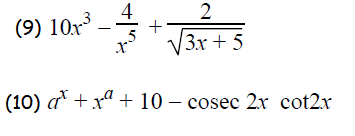
Question 1 :

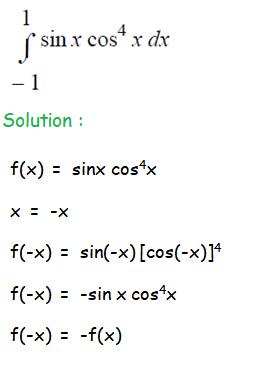
The given function is odd.

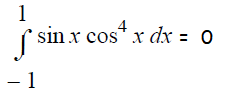
Question 2 :

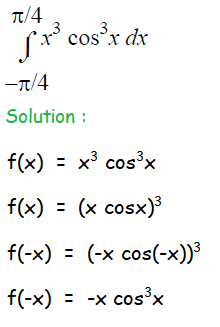
The given function is odd.

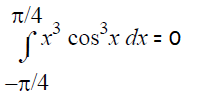
Question 3 :

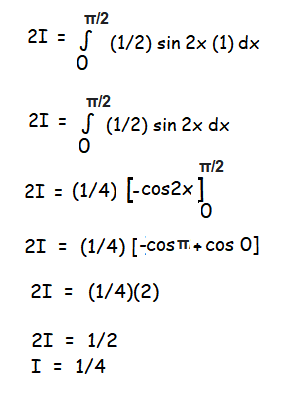
Question 4 :

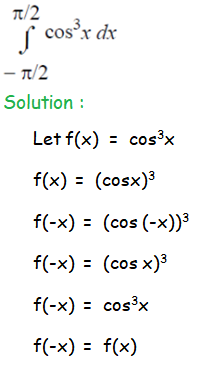
The function f(x) is even.

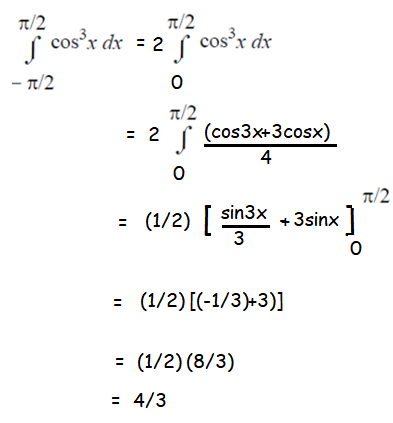
Question 5 :

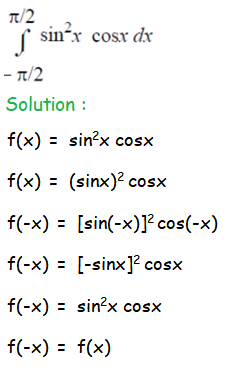
The function f(x) is even.

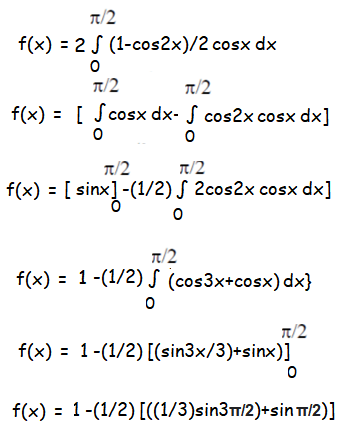
=  1 - (1/2) [-1/3+1]

=  1-(1/2)[2/3]

=  1-(1/3)

=  2/3

Question 6 :

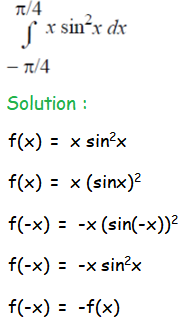
The function f(x) is odd.

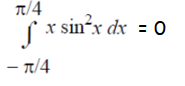
Question 7 :

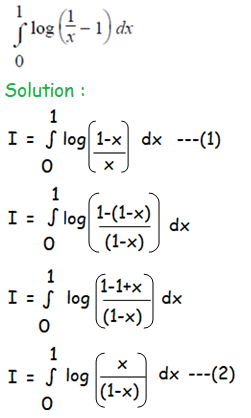
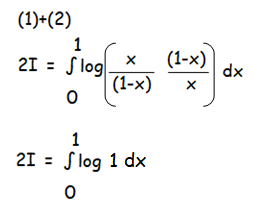
2I  =  0

I  =  0

So, the answer is 0.

Question 8 :

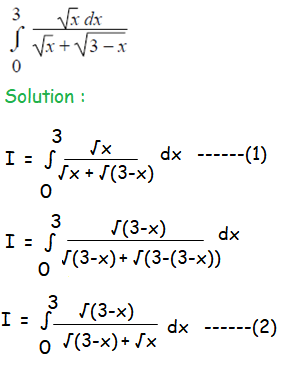
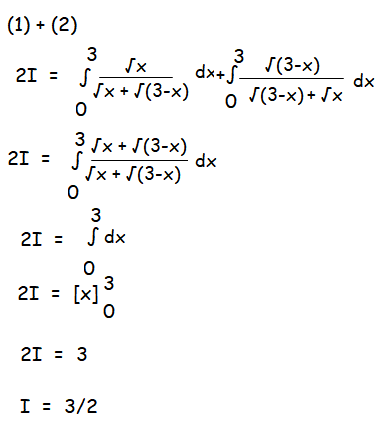
Question 9 :

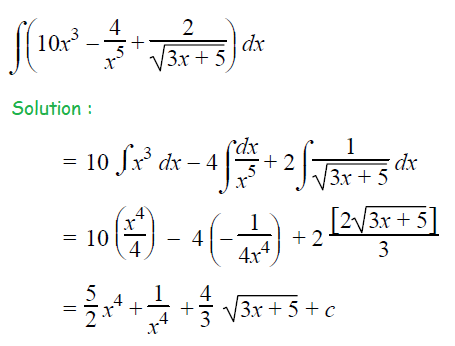
Question 10 :

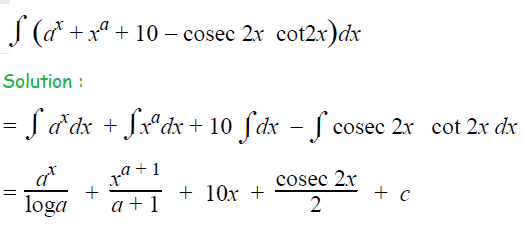
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.