MEDIAN IN STATISTICS
Median is one of the measures of central tendency which can be defined as follows.
Median is the middle-most value when the observations are arranged either in an ascending order or a descending order of magnitude.
For example, if the marks of the 7 students are 72, 85, 56, 80, 65, 52 and 68, then in order to find the median mark, we arrange these observations in the following ascending order of magnitude:
52, 56, 65, 68, 72, 80, 85.
Since the 4th term i.e. 68 in this new arrangement is the middle most value, the median mark is68
i.e. Median (Me) = 68.
As a second example, if the wages of 8 workers, expressed in dollars are 56, 82, 96, 120, 110, 82, 106, 100 then arranging the wages as before, in an ascending order of magnitude, we get $56, $82, $82, $96, $100, $106, $110, $120.
Since there are two middle-most values, namely, $96, and $100 any value between $96 and $100 may be, theoretically, regarded as median wage.
However, to bring uniqueness, we take the arithmetic mean of the two middle-most values, whenever the number of the observations is an even number.
Thus, the median wage in this example, would be
M = (96 + 100) / 2 = 98
If a data set has n items and n is odd, then the median will be the
[(n + 1)/2]th item
If a data set has n items and n is even, then the Median will be the average of
(n/2)th and (n/2 + 1)th items
In case of a grouped frequency distribution, we find median from the cumulative frequency distribution of the variable under consideration.
We may consider the following formula, which can be derived from the basic definition of median.
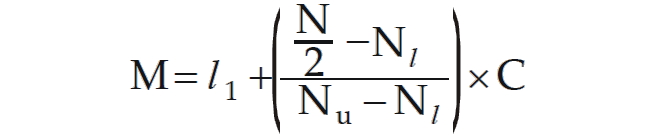
Where,
l1 = lower class boundary of the median class i.e. the class containing median.
N = total frequency.
Nl = less than cumulative frequency corresponding to l₁. (Pre median class)
Nu = less than cumulative frequency corresponding to l₂. (Post median class)
l2 being the upper class boundary of the median class.
C = l2 – l1 = length of the median class.
Example :
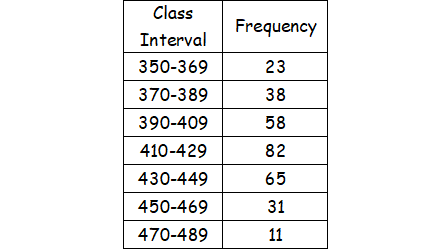
Solution :
Computation of median :
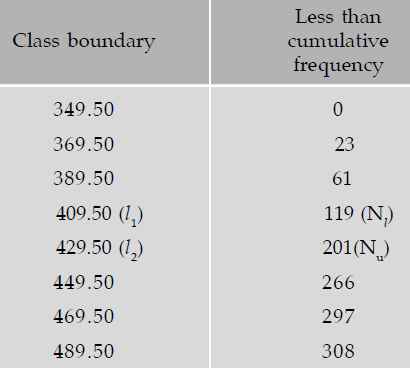
For the given data, the formula to find median is given by
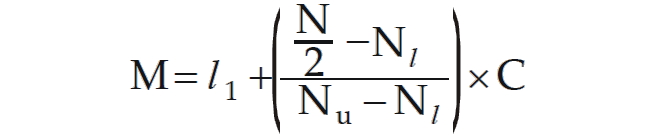
We find, from the table N/2 = 308/2 = 154 lies between the two cumulative frequencies 119 and 201
i.e. 119 < 154 < 201
Thus, we have
Nl = 119
Nu = 201
l1 = 409.50
l2 = 429.50
C = 429.50 – 409.50 = 20
Substitute these values in the above formula.
M = 409.50 + [ (154-119) / (201-119) ] x 20
M = 409.50 + 8.54
M = 418.04
Properties of Median
1) If x and y are two variables, to be related by y=a+bx for any two constants a and b, then the median of y is given by
Mᵧ = a + bMₓ
For example, if the relationship between x and y is given by
2x – 5y = 10
and if the median of x is known to be 16.
Then,
2x – 5y = 10
y = -2 + 0.40x
Now, we have
Mᵧ = -2 + 0.40Mₓ
Mᵧ = -2 + 0.40(16)
Mᵧ = 4.4
2) For a set of observations, the sum of absolute deviations is minimum when the deviations are taken from the median. This property states that ∑|xᵢ–A| is minimum if we choose A as the median.
3) We cannot treat median mathematically, the way we can do with arithmetic mean.
4) It is rigidly defined.
5) It is easy to comprehend.
6) It is not based on all the observations.
7) It is not much affected by sampling fluctuations.
8) It is the most appropriate measure of central tendency for an open-end classification.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Converting Between Polar and Rectangular Coordinates
Apr 23, 24 10:15 AM
Converting Between Polar and Rectangular Coordinates -
Converting Between Polar and Rectangular Equations Homework
Apr 21, 24 08:29 PM
Converting Between Polar and Rectangular Equations Homework -
Converting Between Polar and Rectangular Equations Worksheet
Apr 21, 24 01:23 AM
Converting Between Polar and Rectangular Equations Worksheet
