CONE

Cone is the solid that is generated by rotating a line segment which is passing through a fixed point and making a constant angle with a fixed line.

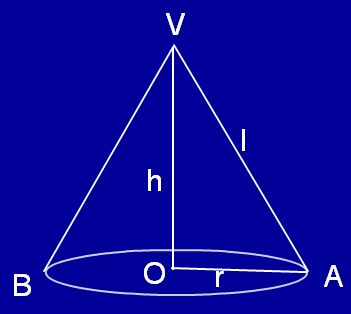
In the above figure here , VO is a fixed line and VA is a rotating line which is making constant angle with VO. The point A would describe a circle with center O such that the line segment VO is perpendicular to the base.

VO is the height h and OA is the base radius r VA is the slant height l.

It is very clear VAO is right angled triangle and the right angle is at at O.

Since VAO is the right angled triangle by Pythagorean theorem

we have l² = h² + r²

If we know the value of the other two measurements.

For example, if we have the height h, and the radius r , we can easily determine the value of the slant height l.

Example 1 :

If the height and radius of a right circular conoid are 4cm and 3cm respectively, find the slant height.

Solution :

Let us plug the known values in to the equation.

l²  =  h² + r²

l²  =  4² + 3²

l²  =  16 + 9

l²  =  25

So, slant height is is 5 cm.

Example 2 :

A heap of paddy is in the form of a conoid whose diameter is 4.2 m and height is 2.8 m. If the heap is to be covered exactly by a canvas to protect it from rain, then find the area of the canvas needed.

Solution :

Diameter of heap of paddy = 4.2 m

r  =  4.2/2

=  2.1 m

height of paddy (h) = 2.8 m

l²  =  r²+h²

l  =  √(2.1)²+(2.8)²

l  =  √(4.41+7.84)

l  =  √12.25

l  =  3.5 cm

Curved surface area of heap of paddy = Π r l

=  (22/7) ⋅ (2.1) ⋅ (3.5)

=  22 ⋅ (2.1) ⋅(0.5)

=  23.1 cm²

Curved surface area of paddy is 23.1 cm².

Example 3 :

Consider the semi-circular piece of paper shown.

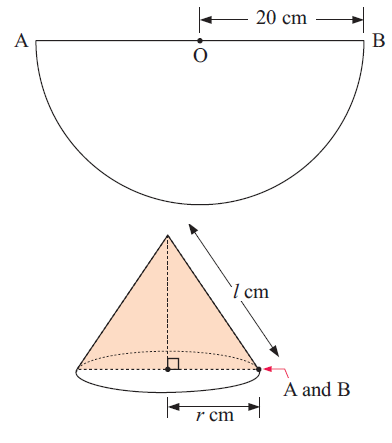
When sides [OA] and [OB] are put together, we form a cone.

a) Find the value of l.

b) Find the circumference of the base of the cone.

c) Use b to find r.

d) Find the area of the base of the cone.

e) Find the area of the curved surface of the cone.

f) Find the total surface area of the cone.

Solution :

(a)  When we rotate the semicircular shape into cone, the radius will become slant height.

Radius of semicircle  =  slant height  =  10 cm

(b)  Circumference of base  =  2πr

=  2 x π x 20

=  40 π

(c)   Circumference of base of cone  =  πr

=  10 π

Radius of base of cone  =  10 cm.

d) Find the area of the base of the cone.

=  πr²

=  π(10)²

=  100π

e) Find the area of the curved surface of the cone.

Curved surface area  =  πrl

=  π(10)(10)

=  100π

f) Find the total surface area of the cone.

=  πr(l+r)

=  π(10)(10+10)

=  200π

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.