CIRCUMCENTER OF A TRIANGLE

The point of concurrency of the perpendicular bisectors of the sides of a triangle is called the circumcenter of the triangle.

The following steps will be useful to find circumcenter of a triangle. 

Step 1 : 

Find the equations of the perpendicular bisectors of any two sides of the triangle. 

Step 2 : 

Solve the two equations found in step 2 for x and y. 

The solution (x, y) is the circumcenter of the triangle given.

Example : 

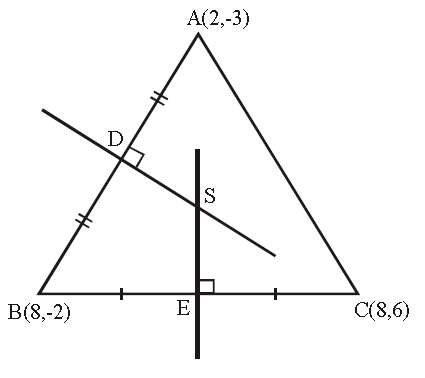
Find the co ordinates of the circumcenter of a triangle whose vertices are (2, -3), (8, -2) and (8, 6).

Solution : 

Let A(2, -3), B(8, -2) and C(8, 6) be the vertices of the triangle. 

D is the midpoint of AB and E is the midpoint of BC. 

Midpoint of AB is

=  [(x₁ + x₂)/2, (y₁ + y₂)/2]

Substitute (x₁, y₁)  =  (2, -3) and (x₂, y₂)  =  (8, -2).

=  [(2 + 8)/2, (-3 - 2)/2]

=  [10/2, -5/2]

=  (5, -5/2)

So, the point D is (5, -5/2). 

Slope of AB is 

=  [(y₂ - y₁)/(x₂ - x₁)]

Substitute (x₁, y₁)  =  (2, -3) and (x₂, y₂)  =  (8, -2).

=  [(-2 - (-3)] / (8 - 2)

=  (-2 + 3) / 6

=  1/6

Slope of the perpendicular line to AB is

=  -1 / slope of AB

=  -1 / (1/6)

=  -1 ⋅ (6/1)

=  -6

Equation of the perpendicular bisector to the side AB :

y  =  mx + b

Substitute  m  =  -6. 

y  =  -6x + b -----(1)

Substitute the point D(5, -5/2) for (x, y) into the above equation. 

-5/2  =  -6(5) + b

-2.5  =  -30 + b

Add 30 to each side. 

27.5  =  b

Substitute b  =  27.5 in (1). 

(1)-----> y  =  -6x + 27.5

Equation of the perpendicular line through D is 

y  =  -6x + 27.5 -----(2)

Midpoint of BC is

=  [(x₁ + x₂)/2, (y₁ + y₂)/2]

Substitute (x₁, y₁)  =  (8, -2) and (x₂, y₂)  =  (8, 6).

=  [(8 + 8)/2, (-2 + 6)/2]

=  [16/2, 4/2]

=  (8, 2)

So, the point E is (8, 2). 

Slope of BC is 

=  [(y₂ - y₁)/(x₂ - x₁)]

Substitute (x₁, y₁)  =  (8, -2) and (x₂, y₂)  =  (8, 6).

=  [6 - (-2)] / (8 - 8)

=  (6 + 2) / 0

=  8/0

Slope of the perpendicular line to BC is

=  -1 / slope of BC

=  -1 / (8/0)

=  -1 ⋅ (0/8)

=  -1 ⋅ 0

=  0

Equation of the perpendicular bisector to the side BC :

y  =  mx + b

Substitute  m  =  0. 

y  =  b -----(3)

Substitute the point E(8, 2) for (x, y) into the above equation. 

2  =  b

Substitute b  =  2 in (1). 

(1)-----> y  =  2

Equation of the perpendicular line through D is 

y  =  2 -----(4)

Solving (2) and (4), we get

x  =  4.25  and  y  =  2

Therefore, the circumcenter of the triangle ABC is 

(4.25, 2)

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.