APPLICATION PROBLEMS ON COEFFICIENT OF VARIATION
Coefficient of variation of a data is obtained by dividing the standard deviation by the arithmetic mean. It is usually expressed in terms of percentage.
This concept is suggested by one of the most prominent Statistician Karl Pearson.
Formula to calculate coefficient of variation from mean and standard deviation is
= (σ/x̄) ⋅ 100%
Here σ is the standard deviation and x̄ is the mean.
Formula to find standard deviation σ is
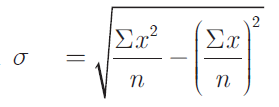
Formula to find arithmetic mean x̄ is
x̄ = ∑x/n
Note :
The data with lesser coefficient of variation is more consistent or stable than the other data.
Problem 1 :
Two marks scored by two students A, B in a class are given below.
A 58 51 60 65 66
B 56 87 88 46 43
who is more consistent ?
Solution :
To check who is more consistent, let us find coefficient of variation for both A and B.
Student A :
x̄ = (Σ x/n)
x̄ = (58+51+60+65+66)/5
= 300/5
= 60
|
x 51 58 60 65 66 |
d = x - 60 51-60 = -9 58-60 = -2 60-60 = 0 65-60 = 5 66-60 = 6 |
d2 81 4 0 25 36 |
Σx = 300 and Σd² = 146
|
σ = √Σd2/n = √146/5 = √29.2 = 5.4 |
C.V = (σ/x̄)⋅ 100 = (5.4/60) ⋅100 = 9 |
Student B :
x̄ = (Σ x/n)
x̄ = (56+87+88+46+43)/5
= 320/5
= 64
|
x 43 46 56 87 88 |
d = x - 64 43-64 = -21 46-64 = -18 56-64 = -8 87-64 = 23 88-64 = 24 |
d² 441 324 64 529 576 |
Σx = 320 and Σd² = 1934
|
σ = √Σd²/n = √1934/5 = √386.8 = 19.67 |
C.V = (σ/x̄) ⋅ 100 = (19.67/64) ⋅ 100 = 30.73 |
Coefficient of variation of student A is less than student B.
So, student A is more consistent than student B.
Problem 2 :
The mean and standard deviation of marks obtained by 40 students of a class in three subjects Mathematics, Science and Social Science are given below
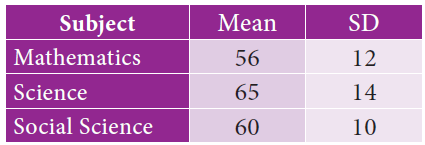
Which of the three subjects shows highest variation and which shows lowest variation in marks?
Solution :
Mathematics :
Coefficient of variation (C.V) = (σ/x̄) ⋅ 100%
x̄ = 56, σ = 12
C.V = (12/56) ⋅ 100%
C.V = 0.2142 ⋅ 100%
C.V = 21.42%
Science :
Coefficient of variation (C.V) = (σ/x̄) ⋅ 100%
x̄ = 65, σ = 14
C.V = (14/65) ⋅ 100%
C.V = 0.2153 ⋅ 100%
C.V = 21.53%
Social Science :
Coefficient of variation (C.V) = (σ/x̄) ⋅ 100%
x̄ = 60, σ = 10
C.V = (10/60) ⋅ 100%
C.V = 0.1666 ⋅ 100%
C.V = 16.66%
The highest variation is in the subject Science and lowest variation is in the subject Social science.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number -
Complex Plane
Apr 14, 24 07:56 AM
Complex Plane