FINDING MISSING LENGTHS IN SIMILAR TRIANGLES

Example 1 :

Find the unknown values of the following figure. All lengths are given in centimeters (all measures are not in scale)

EFCD is a parallelogram, So EF = 7 cm, DE = CF = 6 cm

Solution :

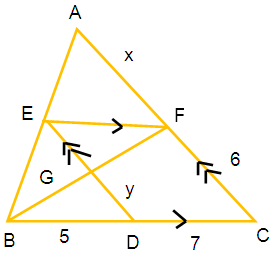
By considering triangles ∆ AEF and ∆ ABC,

 ∠AEF  =  ∠ABC (Corresponding angles)

 ∠A  =  ∠A (common angle)

By using AA similarity criterion ∆ AEF ~ ∆ ABC

(AF/AC)  =  (EF/BC)

[x/(x + 6)]  =  (7/12)

12x  =  7 (x + 6)

12x  =  7x + 42

12x - 7x  =  42

5x  =  42

x  =  42/5

x  =  8.4 cm

Considering the triangles ∆ BDG and ∆ BCF

(BD/BC)  =  (DG/CF)

DG  =  (BD/BC) ⋅ CF

y  =  (5/12) ⋅ 6

y  =  30/12

   =  2.5 cm

Example 2 :

The image of the man of height 1.8 m, is length 1.5 cm on the film of a camera. If the film is 3 cm from the lens of the camera, how far is the man from the camera?

Solution :

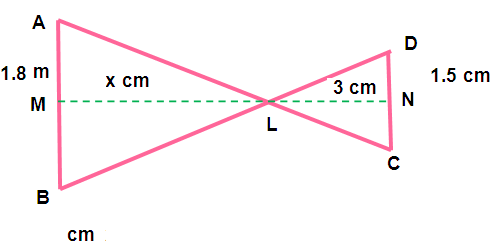
Here AB represents height of man

CD represents height of reflection

Let “L” be the position of lens

LM represents distance between man and lens

LN represents distance between lens and tape.

Also the sides AB is parallel to the side CD, AB  =  1.8 m. CD  =  1.5 m, LN  =  3 cm

From triangles ∆ LAB and ∆ LCD, we get

∠LAB  =  ∠LCD (alternate angles)

∠BLA  =  ∠DLC (vertically opposite angles)

By using AA similarity criterion ∆ LAB ~ ∆ LCD

(AB/CD)  =  (LM/LN)

(180/1.5)  =  (LM/3)

LM  =  (180 x 3)/1.5

LM  =  360 cm

100 cm  =  1 m

LM  =  360/100

LM  =  3.6 m

So the distance between man and camera is 3.6 m

Example 3 :

A girl of height 12 cm is walking away from the base of a lamp post at a speed of 0.6 m/sec . If the lamp is 3.6 m above the ground level, then find the length of her shadow after 4 seconds.

Solution :

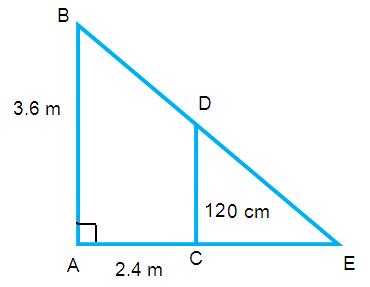
Let AB be the height of lamp. CD be the height of girl and CE be the length of shadow of the girl.

AB  =  3.6 m, CD  =  120 cm  ==>   1.2 m

The girl is walking at the rate of 0.6 m/sec. Now we are going to find the distance traveled by the girl

AC  =  4(0.6)  ==>  2.4 m

From the triangles ECD and EAB the sides CD is parallel to AB.

∠ECD  =  ∠EAB (corresponding angles)

∠E  =  ∠E (common angles)

By using AA similarity criterion ∆ ECD ~ ∆ EAB

(EC/EA)  =  (CD/AB)

[EC/(2.4 + EC)]  =  1.2/3.6

[EC/(2.4 + EC)]  =  1/3

3 EC  =  1 (2.4 + EC)

3 EC  =  2.4 + EC

3 EC – EC  =  2.4

2 EC  =  2.4

EC  =  2.4/2

EC  =  1.2 m

So length of shadow of the girl is 1.2 m.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.