FINDING THE MISSING SIDE LENGTH USING SIMILAR TRIANGLES

Question :

Find the values of x and y in the figure shown below. 

Answer :

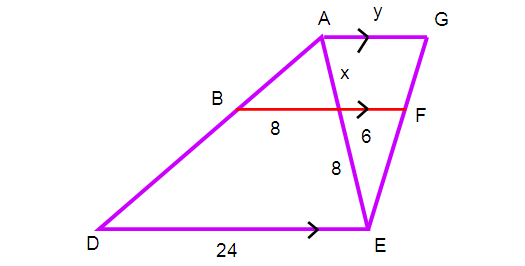
From triangles ABC and triangle ADE

 ∠ABC = ∠ADE (corresponding angles)

∠A = ∠A (common angle)

So ∆ ABC ~ ∆ ADE

(AC/AE)  =  (BC/DE)

[x/(x + 8)]  =  (8/24)

[x/(x + 8)]  =  (1/3)

3 x  =  1 (x + 8)

3 x  =  x + 8

3 x – x  =  8

2 x  =  8

  x  =  8/2

x  =  4 cm.

also ∆ EAG and ∆ ECF are congruent  triangles

So, (EC/EA)  =  (CF/AG)

AG  =  (EA ⋅ CF)/EC

EA  =  EC + CA

  =  8 + 4  ==>  12 cm

y  =  (6 ⋅ 12)/8

 y  =  72/8

  =  9 cm

The values of x and y are 4 and 9 cm respectively.

Example 2 : 

Find the values of x and y in the figure shown below. 

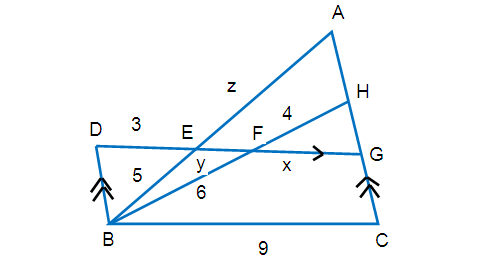
In the diagram shown below, the sides FG and BC are parallel. So, ∆ HFG ~ ∆ HBC. 

Then, 

(HF/HB)  =  (FG/BC)

(4/10)  =  (x/9)

x  =  (4 ⋅ 10)/4

x  =  3.6 cm

In triangle ∆ FBD and ∆FHG the sides BD and GH are parallel,

∠FBD  =  ∠FHG (alternate angles)

∠BFD  =  ∠HFG (vertically opposite angels)

By using AA similarity criterion ∆ FBD ~ ∆ FHG

(FG/FD)  =  (FH/FB)

[x/(y + 3)]  =  (4/6)

3.6/(y + 3)  =  (2/3)

3.6(3)  =  2 (y + 3)

10.8  =  2 y + 6 

2 y  =  10.8 – 6

2 y  =  4.8

   y  =  4..8/2

   y  =  2.4 cm

In triangles ∆ AEG and ∆ ABC, the sides EG and BC are parallel,

∠A  =  ∠A (common angle)

∠AEG  =  ∠ABC (corresponding angles)

By using AA similarity criterion ∆ AEG ~ ∆ ABC

(AE/AB)  =  (EG/BC)

[z/(z + 5 )]  =  (x + y)/9

[z/(z + 5 )]  =  6/9

9 z  =  6 (z + 5)

9 z  =  6 z + 30

9 z – 6 z  =  30

3 z  =  30

  z  =  30/3

   z  =  10 cm

So length of the side FG  =  3.6 cm

Length of the side BF  =  2.4 cm

Length of the side AE  =  10 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.