SIMILAR TRIANGLES WORD PROBLEMS
Problem 1 :
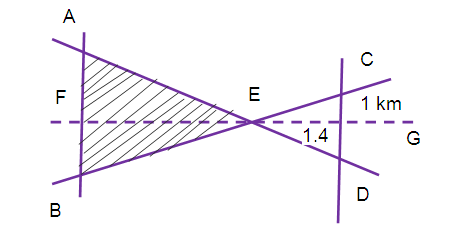
The government plans to develop a new industrial zone in an unused portion of land in a city.
The shaded portion of the map shown given below indicates the area of the new industrial zone. Find the area of the new industrial zone.
Solution :
By considering the lines AD and BC,the angles
∠AEB = ∠DEC (vertically opposite angles)
∠EAB = ∠EDC (alternate angles)
By using AA similarity criterion ∆ EAB ~ ∆ EDC
(AB/DC) = (EF/EG)
EF = (AB/DC) ⋅ EG
= (3/1) ⋅ 1.4
= 4.2 km
Area of new industrial zone = Area of ∆ EAB
= (1/2) ⋅ AB ⋅ EF
= (1/2) x 3 x 4.2
= 6.3 km²
So the area of new industrial zone is 6.3 km²
Problem 2 :
A boy is designing a diamond shaped kite, as shown in the figure where AE = 16 cm, EC = 81 cm. He wants to use a straight cross bar BD. How long should it be?
Solution :
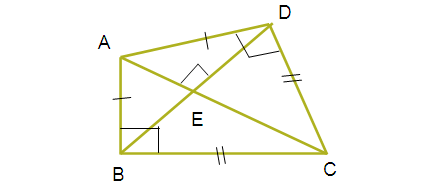
∆ EAD ~ ∆ EDC
So, EA/ED = ED/EC
ED² = EA ⋅ EC
= 16 ⋅ 81
= √16 ⋅ 81
= 4 ⋅ 9
= 36
ABD is the isosceles right triangle and the side AE is perpendicular to the side BD.
BE = ED
So,
BD = 2 ED
= 2(36) ==> 72 cm
Problem 3 :
A student wants to determine the height of flag pole. He placed a small mirror on the ground so that he can see reflection of the top of the flagpole. The distance of the mirror from him is 0.5 m and the distance of the flagpole from the mirror is 3 m .If t he eyes are 1.5 m above the ground level, then find the height of the flagpole (The foot of student, mirror and the foot of flagpole lie along the a straight line)
Solution :
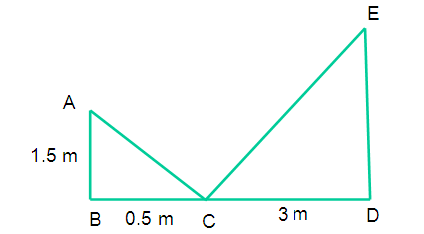
Let “C” be point of reflection
In triangles ABC and EDC
∠ABC = ∠EDC = 90 degree
∠BCA = ∠DCE
By using AA criterion ∆ABC ~ ∆EDC
AB/ED = BC/DC
1.5/ED = 0.5/3
4.5 = 0.5 ED
ED = 4.5/0.5
= 9 m
Therefore height of flag pole = 9 m
Problem 4 :
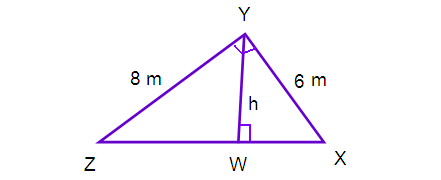
A roof has a cross section as shown in the diagram
(i) Identify the similar triangles
(ii) Find the height h of the roof.
Solution :
Corresponding triangles from the given picture
(i) ∆ WZY ~ ∆ YZX
(ii) ∆ WYX ~ ∆ YZX
(iii) WZY ~ ∆ WYZ
From the (ii)
WY/YZ = XY/XZ
h/8 = 6/10
h = (6/10) ⋅ 8
h = 48/10
h = 4.8 m
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number -
Complex Plane
Apr 14, 24 07:56 AM
Complex Plane