EXAMPLE PROBLEMS ON BASIC PROPORTIONALITY THEOREM

Example 1 :

In a triangle ABC,D and E are points on the sides AB and AC respectively such that DE is parallel to BC.

(i) If AD = 6 cm, DB = 9 cm and AE = 8 cm, then find AC.

Solution :

In the given triangle ABC the sides DE is parallel to the side BC. By using “Thales theorem”, we get

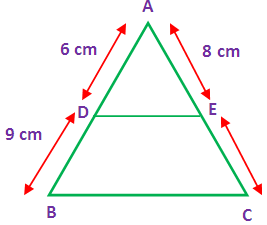
AD/DB = AE/EC

6/9 = 8/EC

EC = (9 ⋅ 8)/6

EC = (3 ⋅ 4)

EC = 12 cm

Example 2 :

In triangle ABC, if AD = 8 cm, AB = 12 cm and AE = 12 cm, then find CE.

Solution :

In the given triangle ABC the sides DE is parallel to the side BC. By using “Thales theorem”, we get

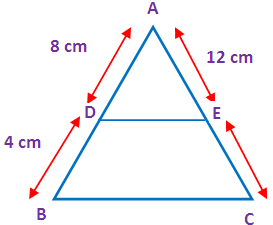
AD/DB = AE/EC

AB = AD + DB

12 = 8 + DB

DB = 4 cm

AD/DB = AE/EC

8/4 = 12/EC

EC = (12 ⋅ 4)/8

EC = 48/8

EC = 6 cm

Example 3 :

In triangle ABC, if AD = 4 x – 3, BD = 3 x – 1, AE = 8 x – 7 and EC = 5 x – 3, then find the value of x.

Solution :

In the given triangle ABC the sides DE is parallel to the side BC. By using “Thales theorem”, we get

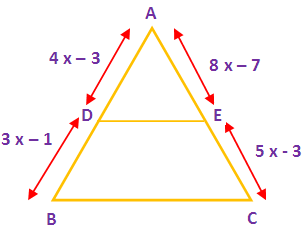
AD/DB = AE/EC

(4x – 3)/(3x – 1) = (8x – 7)/(5x – 3)

(4x – 3)(5x – 3) = (8x – 7)(3x – 1)

20x² – 12x – 15 x + 9 = 24x² – 8x – 21x + 7

 20x² – 24x + 9 =  8x² – 29x + 7

20x² - 24x² – 27x + 29x + 9 – 7 = 0

-4x² + 2 x + 2 = 0

Multiply by -2.

2x² – x - 1 = 0

(x – 1)(2 x + 1) = 0

So the value of x is 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.