SOLVING WORD PROBLEMS USING SUBSTITUTION METHOD

We use the following steps to solve a system of linear equations.

Problem 1 :

Solve 2x  + 3y  =  11 and 2x - 4y  =  -24 and hence find the value of "m" for which y  =  mx + 3.

Solution :

2x + 3y  =  11 ----------- (1)

2x - 4y  =  -24 ----------- (2)

Step 1 :

Find the value of one variable in terms of other variable

3y  =  11 - 2 x

y  =  (11 - 2 x)/3

Let us apply the value of y in (2),

2x - 4(11 - 2x)/3  =  -24

14x - 44  =  -24 (3)

14x - 44  =  -72

 14x  =  -72 + 44

14x  =  - 28

Divide 14 on both sides, we get

x  =  -2

Substitute x  =  -2  in the equation y  =  (11 - 2 x)/3

y  =  [11 - 2(-2)]/3

y  =  15/3

y = 5

Now we have to apply these values in the equation

y   =  m x + 3 

5  =  m (-2) + 3

5  =  -2 m + 3

-2m  =  2

-2 m  =  2

m  =  2/(-2)

m  =  -1

Problem 2 :

The difference between two numbers is 26 and one number is three times the other. Find them

Solution :

Let the two numbers are "x" and "y"

Difference between two number is 26

x - y  =  26 -------- (1)

One number is three times the other

x  =  3 y -------- (2)

Let us apply (2) in (1)

3 y - y  =  26

2 y  =  26

Divide by 2 on both sides, we get

y  =  13

By applying the value of y in (2), we get

x  =  3 (13)

x  =  39

So, required two numbers are 39 and 13.

Problem 3 :

The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them

Solution :

Let the two supplementary angles are "x" and "y"

Sum of these two angles is 180

 x + y  =  180 -----(1)

the larger angle exceeds the smaller by 18

 x  =  y + 18 -----(2)

Now, we are going to apply the value of x in the first equation

y + 18 + y  =  180

2y  =  180 - 18

2y  =  162

y  =  162/2

 y  =  81

 x  =  81 + 18

 x  =  99

So, two supplementary angles are 99 and 81.

Problem 4 :

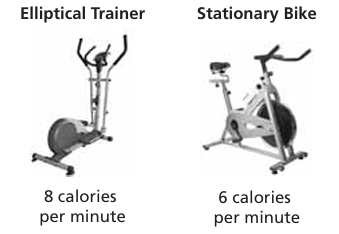
You have 40 minutes to exercise at the gym, and you want to burn 300 calories total using both machines. How much time should you spend on each machine?

Solution :

Let x be the number of minutes you spend in Elliptical trainer.

Let y be the number of minutes you spent in stationary bike.

x + y = 40 ------(1)

8x + 6y = 300------(2)

From (1), y = 40 - x

Applying the value of y in (2), we get

8x + 6(40 - x) = 300

8x + 240 - 6x = 300

2x = 300 - 240

2x = 60

x = 30

Applying the value of x in y = 40 - x

y = 40 - 30

y = 10

You spent 30 minutes in Elliptical trainer and 10 minutes in stationary bike.

Problem 5 :

The sum of the digits of a two-digit number is 11. When the digits are reversed, the number increases by 27. Find the original number

Solution :

Let xy be the required two digit number. Sum of the digits = 11

x + y = 11 -----(1)

When digits are reversed, then xy will become yx.

yx = xy + 27

10y + 1x = 10x + 1y + 27

1x - 10x + 10y - 1y = 27

-9x + 9y = 27

Dividing by 9, we get

-x + y = 3 -----(2)

y = x + 3

Applying the value of y in (1), we get

x + x + 3 = 11

2x = 11 - 3

2x = 8

x = 4

y = 4 + 3

y = 7

So, the required two digit number is 47.

Problem 6 :

A radio station plays a total of 272 pop, rock, and hip-hop songs during a day. The number of pop songs is 3 times the number of rock songs. The number of hip-hop songs is 32 more than the number of rock songs. How many of each type of song does the radio station play?

Solution :

Let x be the number of rock songs and y be the number of pop songs.

y = 3x --------(1)

Number of hip-hop songs = x + 32

x + y + x + 32 = 272

2x + y = 272 - 32

2x + y = 240 --------(2)

Applying the value of y in (2), we get

2x + 3x = 240

5x = 240

x = 240/5

x = 48

y = 3(48)

y = 144

Number of rock songs = 48

Number of pop songs = 144

Number of hip-hop songs = 48 + 32 ==> 80

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.